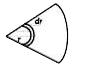
The distance between the vertex and the center of mass of a uniform solid planar circular segment of angular size θ and radius R is given by -

43Rsin(θ/2)θ
Rsin(θ/2)θ
43Rcos(θ2)
23Rcos(θ)
The correct Answer is:A
XCM=∫dmrsinθ/2θ/2∫dm[dm=σrθdr]
=2σsinθ/2∫R0r2drσθ∫R0rdr⇒43Rsin(θ/2)θ
Similar Questions
Distance of the centre of mass of a solid uniform cone from its vertex is z0. It the radius of its base is R and its height is h then z0 is equal to:
View SolutionDistance of the centre of mass of a solid uniform cone from its vertex is z0. It the radius of its base is R and its height is h then z0 is equal to:
View SolutionFind the center of mass of that uniform disk of radius a from which a circular segment of radius b is cut out. The center of the hole is at a distance c from the center of the swatch.
View Solutionकथन l : R त्रिज्या की गोल आकार की स्थिर धरातल पर लुढ़क रही वस्तु के द्रव्यमान केन्द्र के वेग का परिमाण ωR से दिया जाता है। जहाँ ω इसका कोणीय वेग है।
कथन 2 : जब द्रव्यमान वितरण समरूप हो तो गोल आकार की वस्तु का केन्द्र इसका द्रव्यमान केन्द्र होगा।
View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x_(2) of the center of mass of the remaining part from the initial center of mass O is given by
View SolutionA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
View Solutionद्रव्यमान M और त्रिज्या R के एक ठोस गोले में, R2 त्रिज्या की एक गोलीय गुहिका इस प्रकार बनाई गई है कि गुहिका का केंद्र गोले के केंद्र से से R2 दूरी पर है। एक बिंदु द्रव्यमान m को गोले के केंद्र से R4 की दूरी पर गुहिका के अंदर रखा जाता है। गोले और बिंदु द्रव्यमान m के बीच गुरुत्वाकर्षण खिंचाव है
View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View Solution
