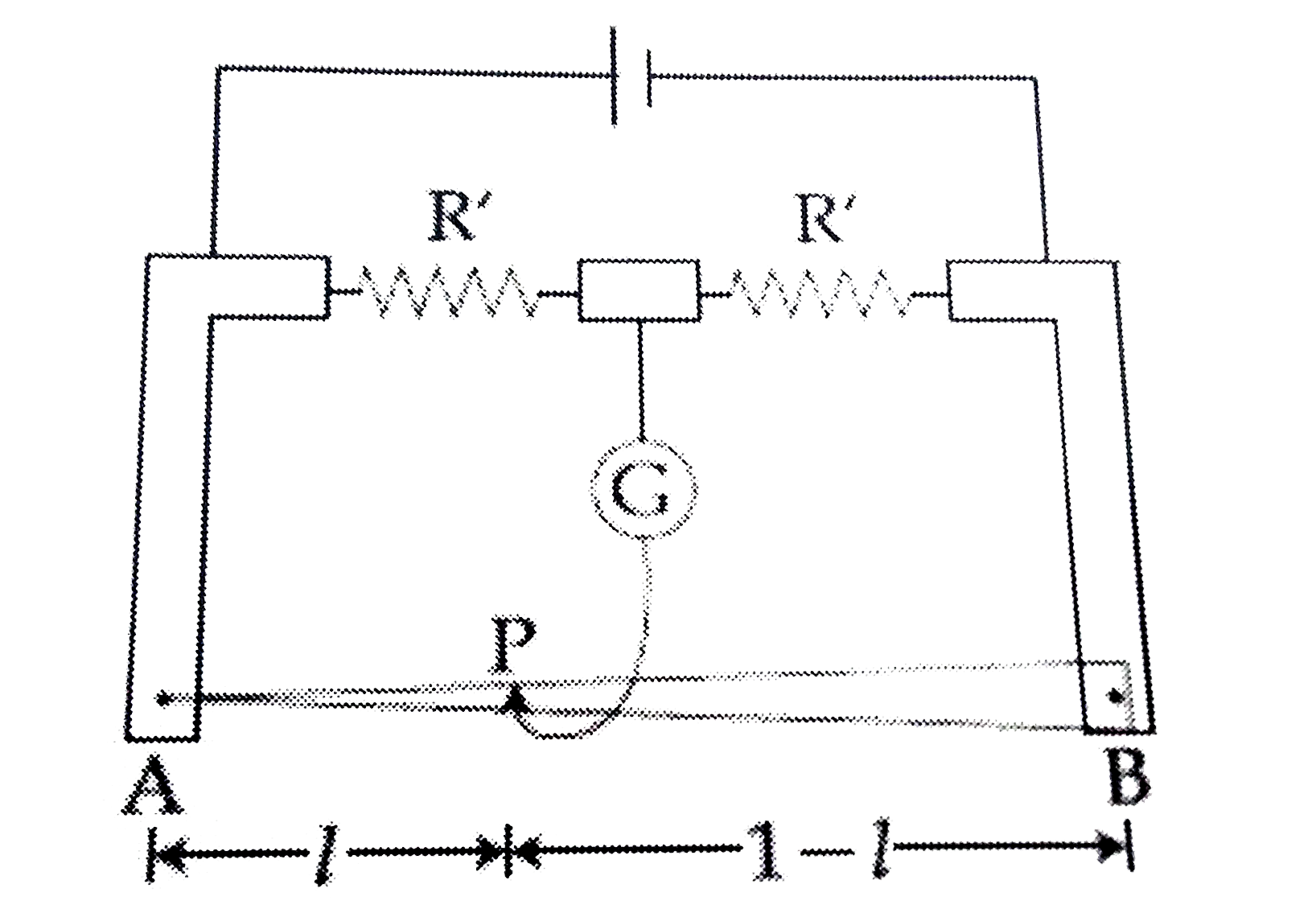
In a meter bridge, the wire of length 1 m has a non- uniform cross - section such that , the variation dRdl of its resistance R with length l is dRdl∝1√l ,Two equal resistances are connected as shown in the figure , the galvanometer has zero deflection when the jockey is at point P, what is the length Ap?
0.2 m
0.3 m
0.25 m
0.35m
The correct Answer is:C
dR=cdl√l
According to Question-
∫l0cdl√l=∫1lcdl√l
(2√l)10=(2√l)1l⇒2√l=2−2√l
4√l=2⇒I=14=0.25m
Similar Questions
In a meter bridge, the wire of length 1 m has a non- uniform cross - section such that , the variation (dR)/(dl) of its resistance R with length l is (dR)/(dl) prop (1)/(sqrt(l)) ,Two equal resistances are connected as shown in the figure , the galvanometer has zero deflection when the jockey is at point P, what is the length Ap?
View SolutionA wire of length l and area of cross-section A has thermal resistance R. What will be its thermal resistance if it is symmetrically folded n times ?
View SolutionIf l=length, R=resistance and A=cross sectional area, then . . . .
View SolutionA uniform wire of resistance R and length L is cut into four equal parts, each of length L/4, which are then connected in parallel. The effective resistance of the combination is
View SolutionA meter bridge setup is shown in the figure. If there is null deflection in galvanometer when length AC = 20 cm, then the value of resistance R is
View SolutionA wire of uniform area of cross section 'a' and length 'l' and resistance 'R' cut into three equal parts. The resistance of each part.
View SolutionA wire of uniform area of cross-section a, length L and resistance R is cut at the middle into two equal parts of length L/2 each .Then the resistivity of each piece compared to that of the original becomes
View SolutionA wire of uniform cross-section and length I has a resistance of 4Omega . The wire is cut into four equal pieces. Each piece is then stretched to length 'l'. Thereafter, the four wires are joined in parallel. Calculate the net resistance.
View Solution