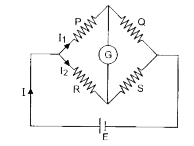
In the Wheatstone bridge shown below, in order to balance the bridge, we must have-

A
B
C
= any finite value
D
any finite value
Video Solution
Text Solution
The correct Answer is:D
The bridge ABCD is balanced if
As no current flows in arm BD
= any finite value.
|
Similar Questions
संतुलित व्हीटस्टोन सेतु क्या है ? संतुलित व्हीटस्टोन सेतु के लिए स्थिति उतपन्न कीजिए |
View SolutionObtain the balancing condition for the Wheatstone bridge arrangement as shown in Figure 4 below:
View SolutionWhen a Wheatstone Bridge will be balanced?
View SolutionWhen a Wheatstone bridge is said to be balanced ?
View SolutionWhen is a Wheatstone bridge called balanced?
View SolutionWhen is a Wheatstone bridge said to be balanced?
View SolutionWhat is Wheatstone bridge? Deduce the condition for which Wheatstone bridge is balanced.
View SolutionWheatstone Bridge#!#Balanced Wheatstone#!#Unbalanced Wheatstone
View Solution