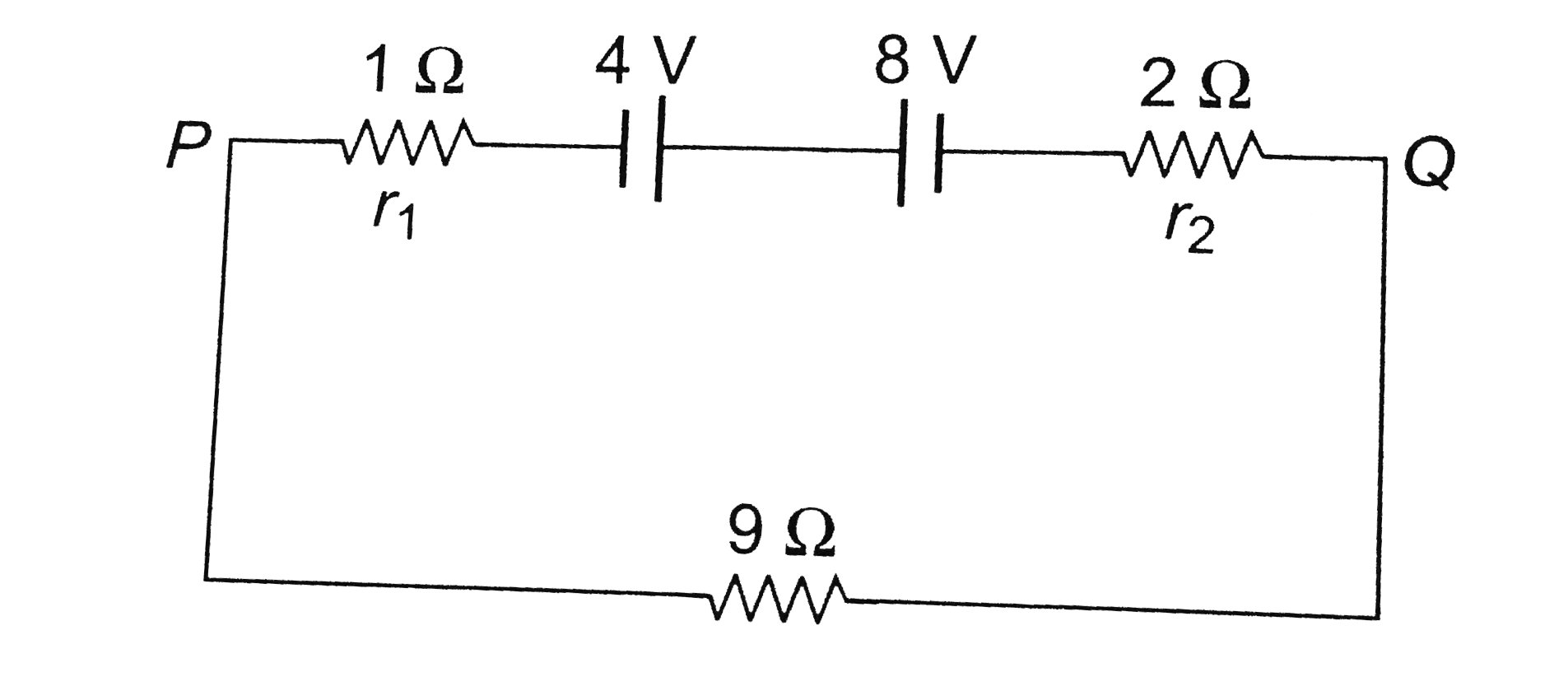
Two batteries of e.m.f. 4V and 8V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q
13A and 3 V
16A and 4 V
19A and 9V
12 A and 12 V
The correct Answer is:A
I=8−42+1+9=412=13A
VP=1×13+4−8+2×13=VQ
⇒VP−VQ=4−1=3V
Similar Questions
Two non-ideal batteries have e.m.f 2V and 8V respectively and internal resistance 1 Omega and 2 Omega respectively as shown in the figure. If the potential difference between a and b is zero then the resistance R has a value
_PHY_E01_014_Q01.png)
View SolutionTwo batteries A and B each of e.m.f. 2V are connected in series to an external resistance R=1Ω. If the internal resistance of battery A is 1.9Ω and that of B is 0.9Ω. What is the potential difference between the terminals of battery A ?
View SolutionA battery has e.m.f. 4V and internal resistance r . When this battery is connected to an external resistance of 2 Omega , a current of 1A flows in the circuit. How much current will flow if the terminals of the battery are connected directly.
View SolutionIf in the circuit shown below
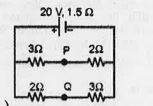 , the internal resistance of the battery is 1.5Ω and VP and VQ are the potentials at P and Q respectively, the potential difference between the points P and Q is
, the internal resistance of the battery is 1.5Ω and VP and VQ are the potentials at P and Q respectively, the potential difference between the points P and Q is
View SolutionTwo batteries of e.m.f. 4V and 8V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q

View SolutionA cell of e.m.f. 2V and internal resistance 1.2. Omega is connected with an ammeter of resistance 0.8 Omega and two resistors of 4.5 Omega and 9 Omega as shown in the diagram below: What is the potential difference across the terminals of the cell?
View SolutionIf a battery of emf 8V and netgligible internal resistance in connected between terminals P and Q of the circuit shown in fig 5.225 calculate the current through 2.5 Omega resistance and hence calculate the equivalent resistance of the circuit.
View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

View Solution
