A wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

623A and 1823 A
526A and 1526 A
425 A and 1225 A
325A and 925A
The correct Answer is:A
I=3I+2.5×7.510=2423A
I1=7.510×2423=1823A
I−I1
I2=623A
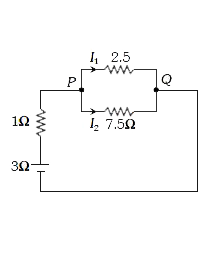
Similar Questions
The terminals of a 18 V battery with an internal resistance of 24 Omega are connected to a circular wire of resistance 24Omega at two point distant at one quarter of the circumference of a circular wire . The current through the bigger arc of the circle will be
View SolutionA wire is bent in the form of circle of radius 2m. Resistance per unit length of wire is 1πΩm. Battery of 6 V is connected between A and B ∠AOB=90∘ . Find the current through the battery.

View SolutionA wire having resistance 20 Omega is bent in the form of a circle as shown in the following figure: What will be the resistance between two end points A and B located on the diameter?
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
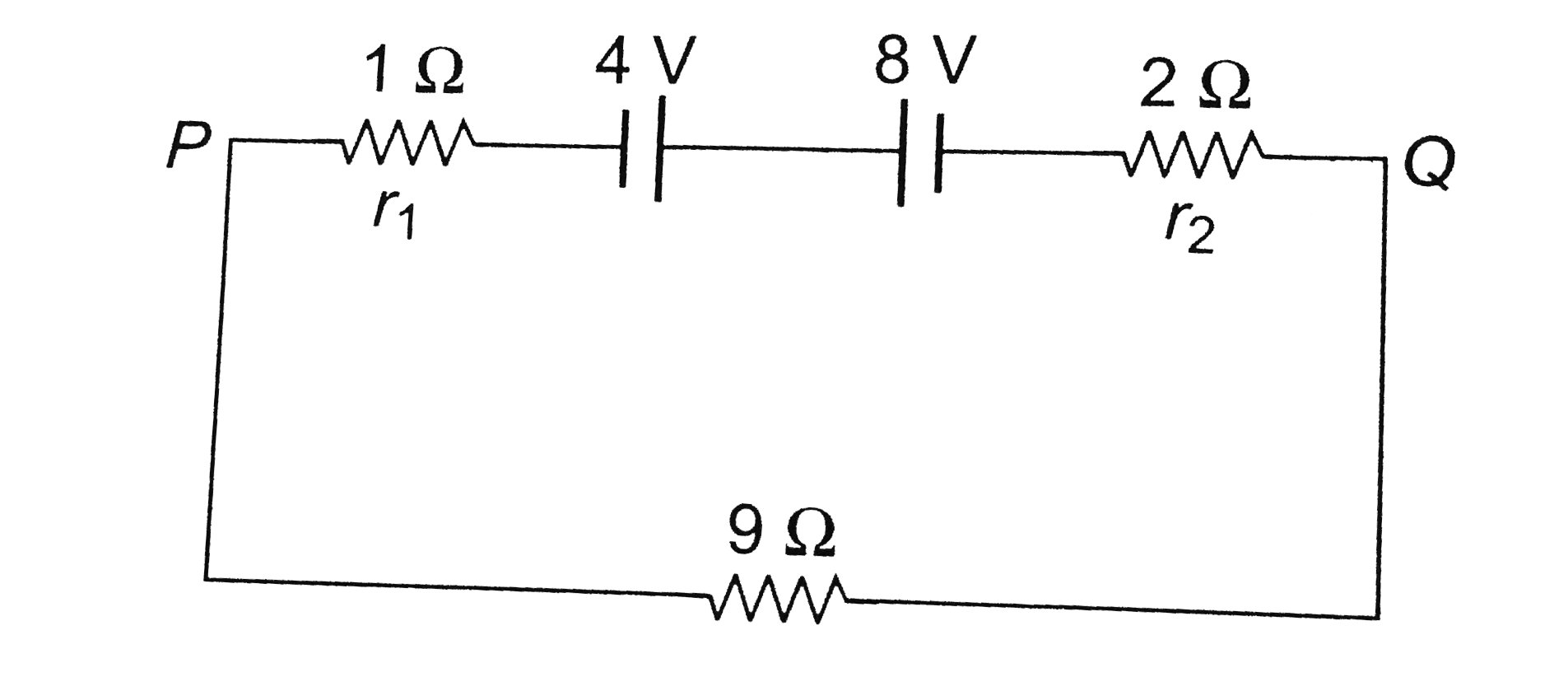
View SolutionTwo batteries of e.m.f. 4V and 8V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q
View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

View SolutionA uniform wire os resistance 12 Omega is bent to form a circle. Effective resistance across two diametrically opposite points is
View SolutionA wire of resistance 20 Omega is bent to form a complete circle. The resistance between two diametrically opposite points A and B as shown in the figure, is
View Solution
