Question

In figure shows a rectangular block with dimensions x , 2 x and 4 x . Electrical contacts can be made to the block between opposite pairs of faces (for example, between the faces labelled A - A , B - B and C - C ). Between which two faces would the maximum electrical resistance be obtained ( A - A : Top and bottom faces, B - B : Left and right faces, C - C : Front and rear faces)

Options

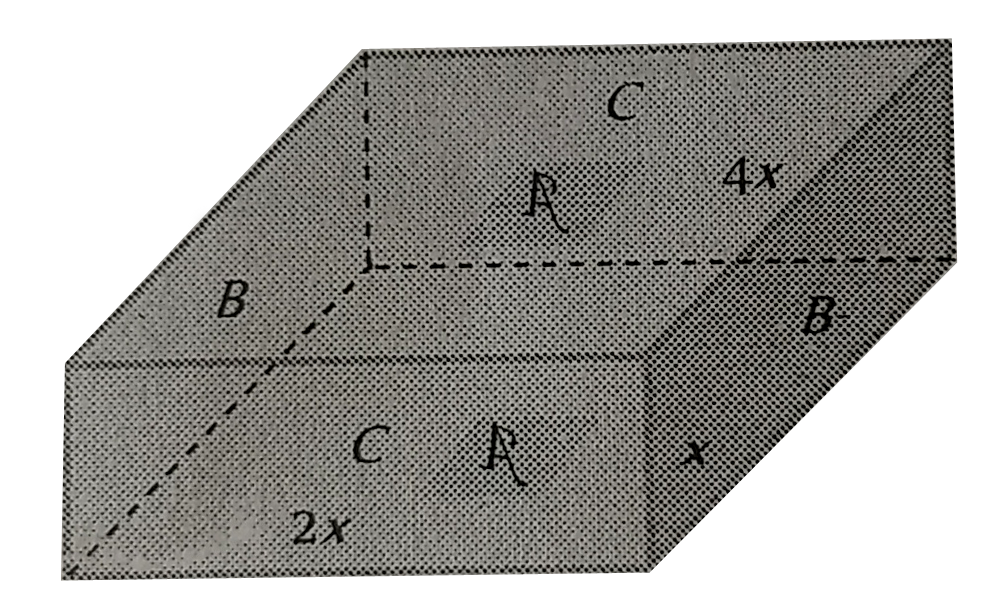
A. A-A
B. B-B
C. C-C
D. Same for all three pairs

Answer

C

Explanation

`R = (rho l)/A`
`I to` maximum `rArr l =4x`
`A to` minimum `rArr A = x xx 2x = 2x^(2)`
`therefore` for face C - C, R will be maximum.