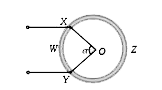
A wire of resistor R is bent into a circular ring of radius r. Equivalent resistance between two points X and Y on its circumference, when angle XOY is a, can be given by-
Rα4π2(2π−α)
R2π(2π−α)
R(2π−α)
4πRα(2π−α)
The correct Answer is:A
Since, I=rθ=rα
Length of arc. XWY = rα
Resistance of arc. XZY = R2πr×ar=Rα2π
Resistance of arc XZY =R2πr×r(2πr)×αr=Rα(2π−α)4π2
Similar Questions
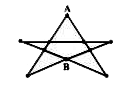
किन्ही दो संलग्न बिंदुओं के मध्य सभी तारों का प्रतिरोध R है। तब चित्र में दर्शाए गए A व B के मध्य तुल्य प्रतिरोध है :
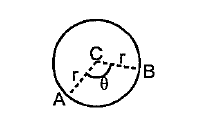
View Solutionएक बैटरी त्रिज्या r और प्रतिरोध R के एकसमान चालक वलय की परिधि पर दो बिंदुओं A और B के बीच जुड़ी हुई है। वलय के चापों में से एक AB केंद्र पर θ कोण अंतरित करता है। वलय में धारा के कारण केंद्र पर चुंबकीय प्रेरण का मान है
View SolutionA and B are two points on a circular ring made of uniform wire of resistane R. If the part AB of the ring subtends an angle θ at the centre C of the ring as shown below, find the resistance of the ring between the points A and B.
View SolutionA wire of resistance R is bent in the form of a cicle. The resistance between two points on the circumstance of the wire and at the end of a daimeter of the circle is :
View SolutionWhen two resistors of resistance R are connected in parallel then the equivalent resistance will be
View SolutionWhen two resistors of resistance R and 2R are connected in parallel then the equivalent resistance is
View SolutionAssertion : A wire of resistance R is bent in the form of a circle. The resistance between two points on circumference or the wire oe at the end of diameter is R/4. Reason : The resistance between the two points on circumference of the circle will be the parallel combination of two resistances of upper and lower parts of the circle.
View SolutionStatement-I: A wire of resistance R is bent in the form of a circle. The resistance between two points on circumference or the wire or at the end of diameter is R/4.
Statement- II: The resistance between the two points on circumference of the circle will be the parallel combination of two resistances of upper and lower parts of the circle.
View Solution
