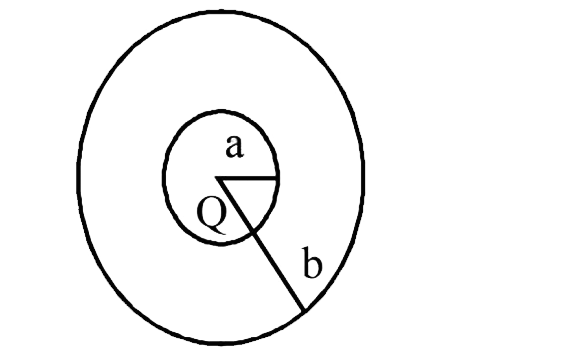
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
Q2π(b2−a2)
2Qπ(a2−b2)
2Qπa2
Q2πa2
The correct Answer is:D
ρ=Ar
According to gauss.s law
∮→E.→ds=qε0
⇒E×4πr2=Q+∫raAr4πr2drε0
⇒E=Q+2πAr2−2πAa24πε0r2
Make E independent of r
Q−2πAa2=0
⇒A=Q2πa2.

Similar Questions
Charge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionA system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View SolutionA system consists of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density rho=alpha/r , where alpha is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
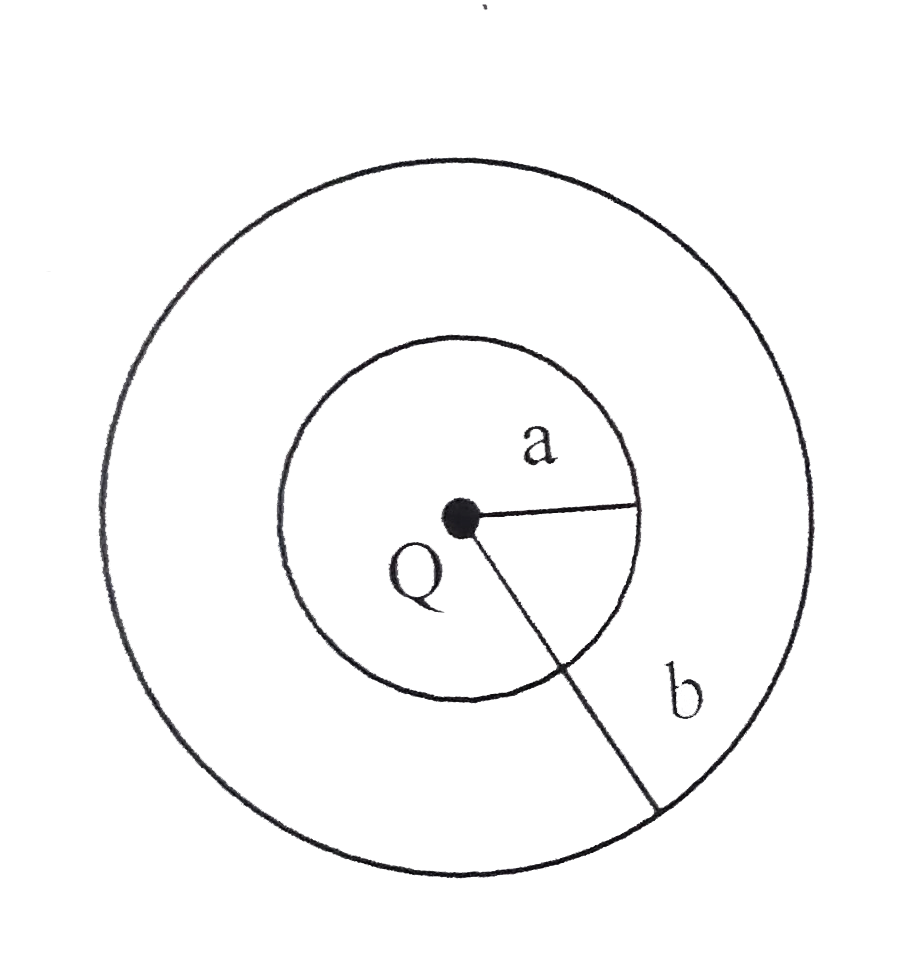
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively(see figure), has volume charge density ρ=Ar , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
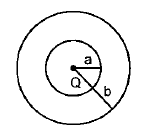
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

View SolutionAn insulating solid sphere of radius R is charged unequally such that the volume charge density rho=(A)/(r ) where A is a positive constant and r is the distance from the centre. The potential difference between the center and the surface of the sphere is:
View Solution
