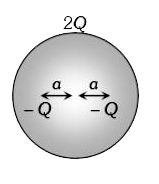
Let a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
a=3R21/4
a=2−1/4R
a=8−1/4R
a=R/√3
The correct Answer is:C
R∫0kr4πr2dr=2Q
kπR4=2Q
KQ24a2=KQa∫0kr4πr2dra2
KQ24a2=QKk4πa24
KQ24a2=QK(2QR4)a2
R=a81/4.
Similar Questions
A sphere of radius R, is charged uniformly with total charge Q. Then correct statement for electric field is (r = distance from centre): -
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View Solutionकुल आवेश 2Q को त्रिज्या R के गोले में इस प्रकार वितरित करते है कि आवेश घनत्व सम्बन्ध ρ(r)=kr से दिया जाता है, जहाँ r केन्द्र से दूरी है। दो बराबर - Q आवेशों A तथा B को केन्द्र से a दूरी पर व्यासीय विपरीत बिन्दुओं पर रखा गया है। यदि A और B कोई बल अनुभव नहीं करते है, तो
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionLet a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
View SolutionA solid sphere of radius R has total charge 2Q and volume charge density p=kr where r is distance from centre. Now charges Q and −Q are placed diametrically opposite at distance 2a where a is distance form centre of sphere such that net force on charge Q is zero then relation between a and R is
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View Solution