The combination of capacitors with C1=3μF,C2=4μFandC3=2μF is charged by connecting AB to a battery.
Consider the following statements
I. Energy stored in C1 = Energy stored in C2 + Energy stored in C3
II. Charge on C1= Charge on C2+ Charge on C3
III. Potential drop across C1= Potential drop across C2= Potential drop across C3
Which of these is/are correct

I and II
II only
I and III
III only
The correct Answer is:B

CAB=3×69=2μF
Q=CABV=2VμC
Q1=Q2+Q3→ correct → (II)
V1=69×V=2V3,V2=V3=V3→ incorrect (III)
U1=12C1V21=2V23,U2=12C2V22=2V29
U3=12C3V23=V29
∴U2+U3=V23≠U1→(I)→ incorrect.
Similar Questions
Calculate the potential difference and the energy stored in the capacitor C_2 in the circuit shown in the Fig. Given potential at A is 90 V , C_1 = 20 mu F , C_2 = 30 mu F and C_3 = 15 mu F
View SolutionCapacitors are devices used to store charges, Capacitors in series:- If three capacitances C_1, C_2 and C_3' are connected in series.what is the Effective capacitance of the combination.
View SolutionTwo capacitors C1 and C2 are connected in series : I) Draw a diagram of the above combination. II) If [C_1 = 4µF, C_2 = 6µF and C_3 = 2.4µF] and a potential difference of 100V is applied across the combination. Calculate the charge stored in each capacitor.
View SolutionThree capacitors C_1 = 3muF, C_2 = 6muF and C_3 = 10muF are connected to a 50 V battery as shown in the figure below: Calculate : The charge on C_1
View Solutionif sin4αcos2α=3∑k=0ckcos2kα then c1+c3=….c0+c2=…..andc0+c1+c2+c3=…….are
View SolutionAnalyze the circuit, find the charge in capactiors C1C2, and C3 in steady state.
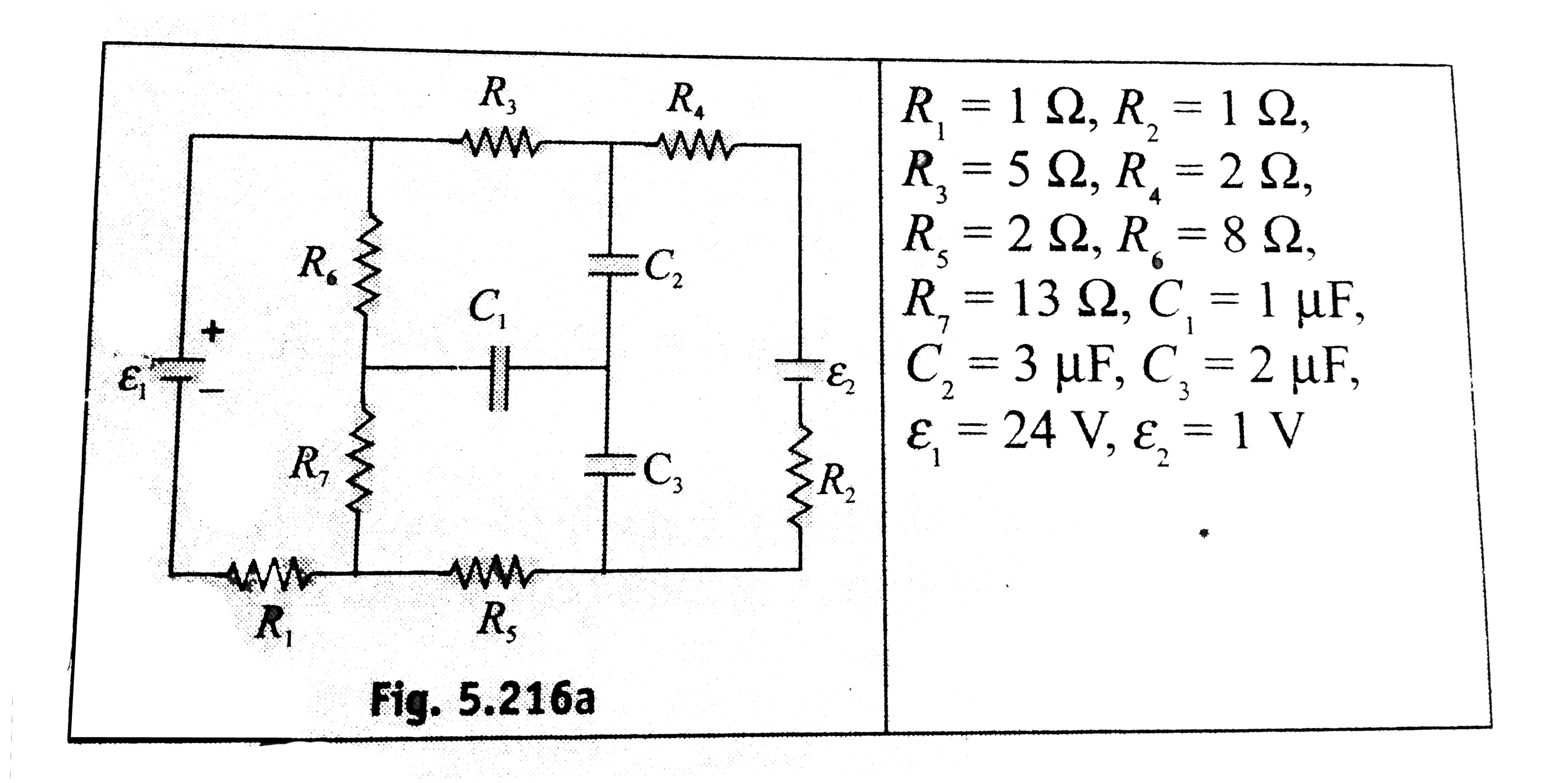
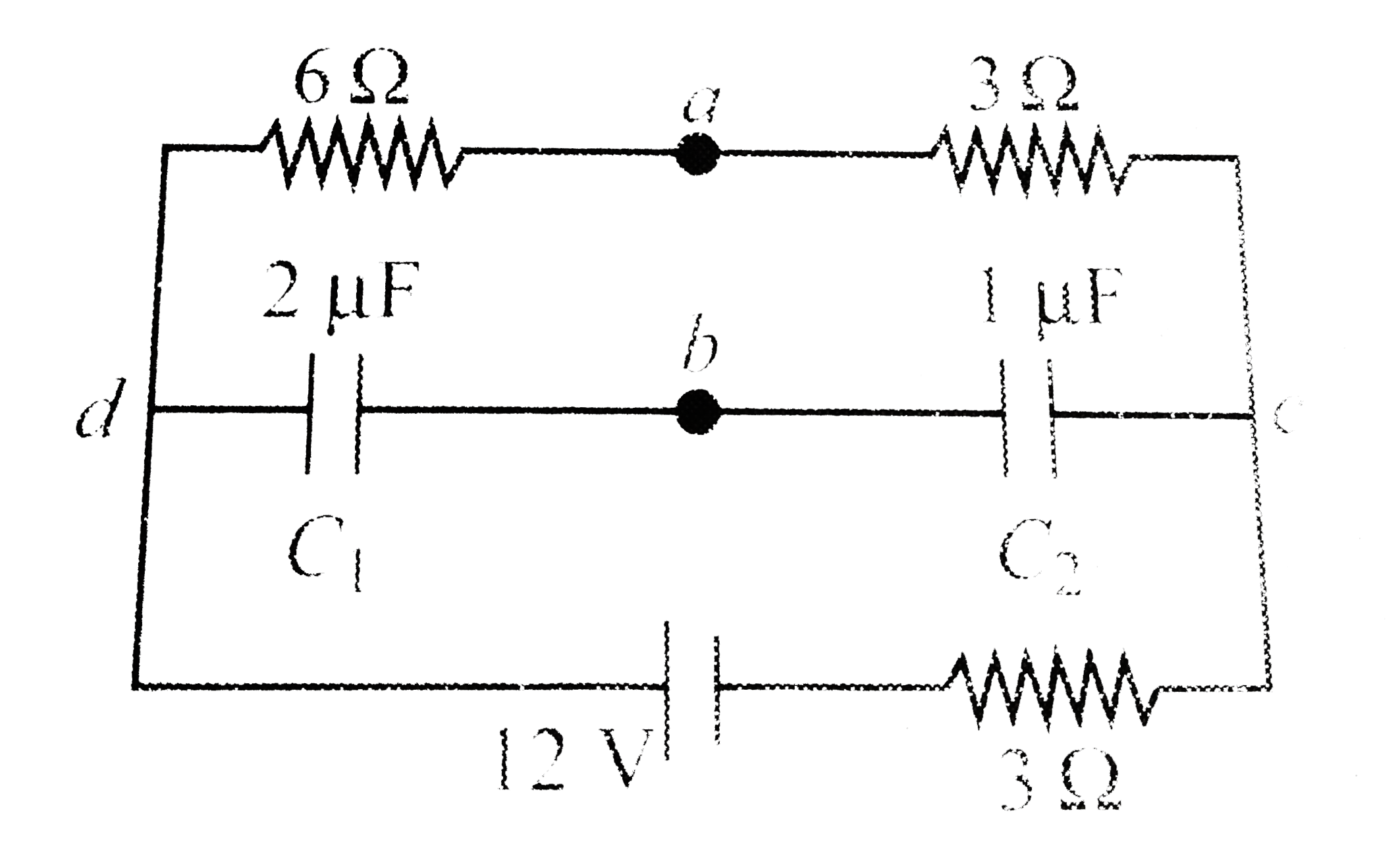
View Solutionwhat is the charge stored on each capacitor C1andC2 in the circuit shown in fig.
View Solutiony=c1x+c2sin(2x+c3) (C1,C2,C3 are arbitrary constants)
View Solution