It is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss’s theorem because
Gauss’s law fails in this case
This problem does not have spherical symmetry
Coulomb’s law is more fundamental than Gauss’s law
Spherical Gaussian surface will alter the dipole moment
The correct Answer is:B
Gauss’s law is applicable for symmetrical body.
Similar Questions
Using Gauss’s theorem, it can be proved that the strength of electric field, at any point, inside a spherical shell is zero. What about the potential at a point ?
View SolutionIt is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss's theorem because:
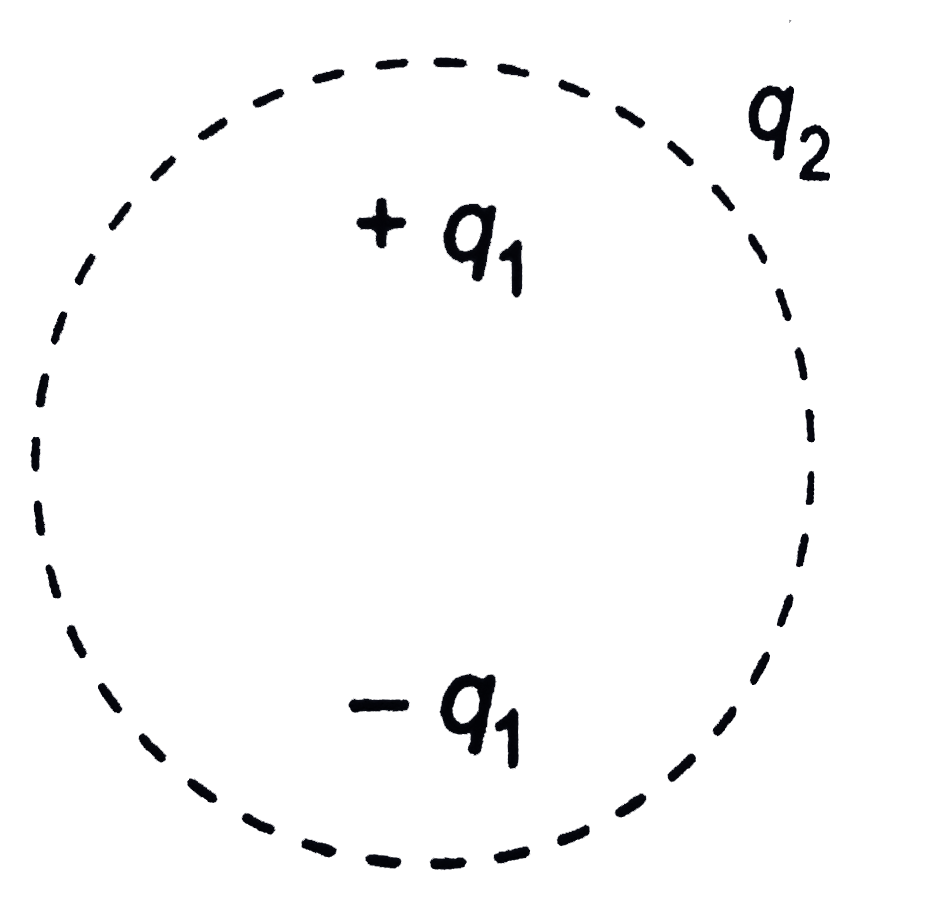
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
View SolutionState the Gauss’s theorem. Findout the expression for electric field’ inside and outside ofa spherical shell.
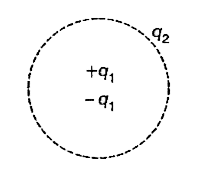
View Solutionचित्र में दर्शाए गए आवेश विन्यास व गोलीय गॉसियन सतह पर विचार कीजिए गोलीय सतह से विधुत क्षेत्र के फ्लक्स की गणना में विधुत क्षेत्र उत्पन्न होगा,
View Solutionगॉस की प्रमेय का उपयोग करके विधुत द्विध्रुव के कारण विधुत क्षेत्र की तीव्रता ज्ञात करने के लिए गोलीय गॉसियन सतह लेता सुविधाजनक नहीं है क्योंकि
View SolutionUsing Gauss's theorem derive an expression for electric field intensity at a point due to -uniformly charged spherical shell.
View Solution
