Assume that an electric field exists in space. Then the potential difference , where is the potential at the origin and the potential at is:
120 V
80 V
The correct Answer is:C
Volt.
Similar Questions
Assum that an electric field →E=30x2ˆiexists in space. Then the potential difference VA−V0, where V0 the potential at the origin and VA the potential at x = 2 m is :
View SolutionAn electric field →E=−−−−−−−→i20+→j30NC−1 exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
View SolutionA uniform electric field to 100 Vm−1 is directed at 60∘ with the positive x-axis as shown in figure. If OA= 2 m, the potential difference VO−VA is
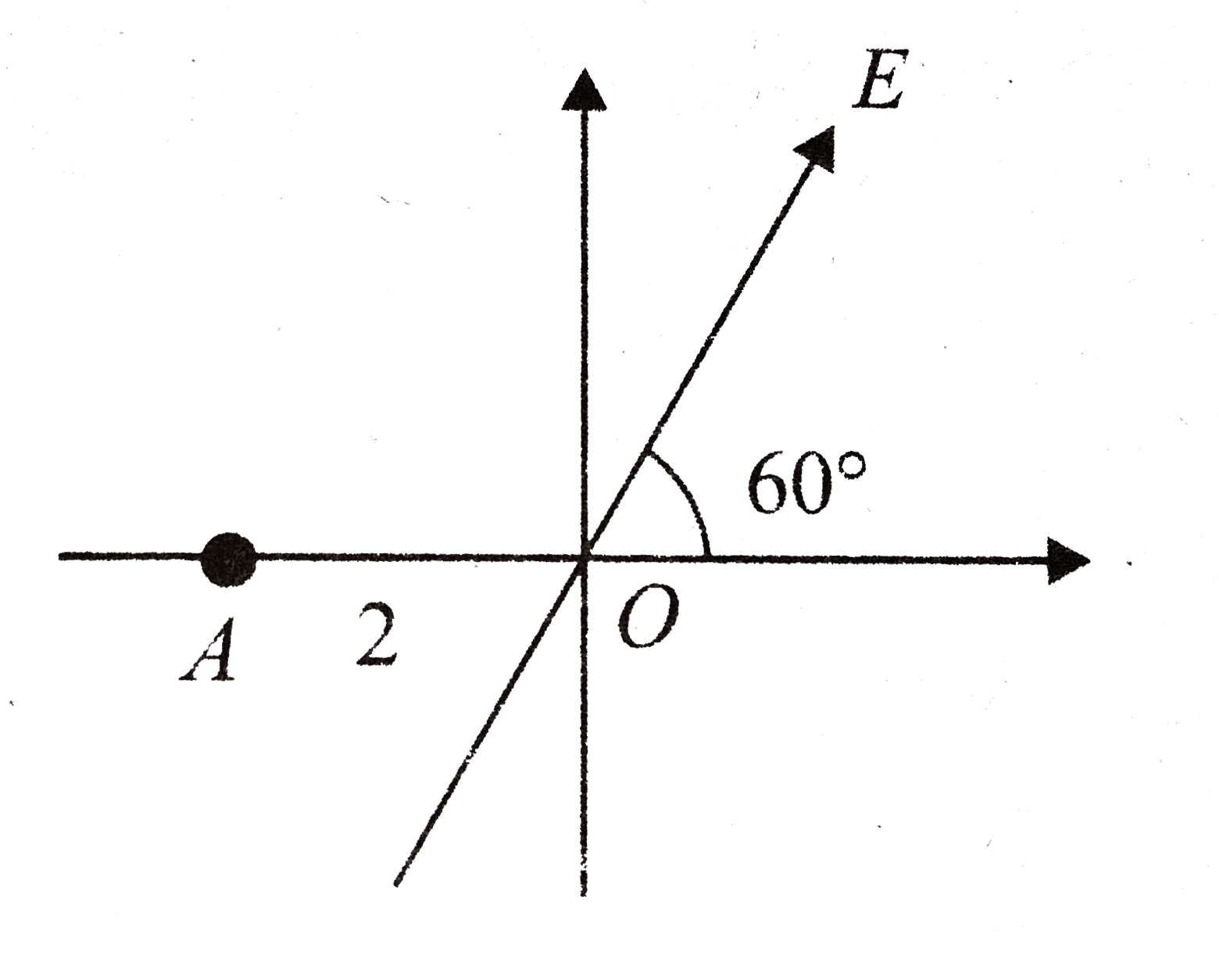
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−V0, where V0 is the potential at the origin and VA the potential at x = 2 m is :
View SolutionThe de - Broglie wavelength of a particle accelerated with 150 v_o potential is 10^(-10) m . If it is accelerated by 600 v_o , its wavelength will be
View Solutionan electric field in space, vecE = 10x hati N C^(-1) is present, where x is measured in meters. Assuming the potential at (10 m, 20 m) to be zero, the potential at the origin is:
View Solution