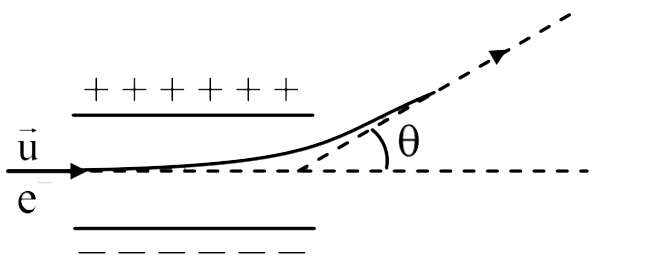
An electron enters a parallel plate capacitor with horizontal speed u and is fond to deflect by angle θ on leaving the capacitor as shown. It is found that tanθ=0.4 and gravity is negligible
If the initial horizontal speed is doubled, then tanθ will be
0.1
0.2
0.8
1.6
The correct Answer is:A
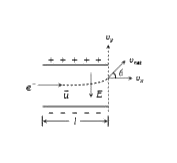
Horizontal displacement = l
Time (t)=lu
Now, vy=uy+at
⇒vy=0+eEm×lu
vy=eElmu
vx remain same ⇒vx=u
tanθ=vyvx=eElmu×1u=eElmu2⇒tanθ∝1u2
When speed u is doubled then tanθ will become 14th
tanθ=0.44=0.1
Similar Questions
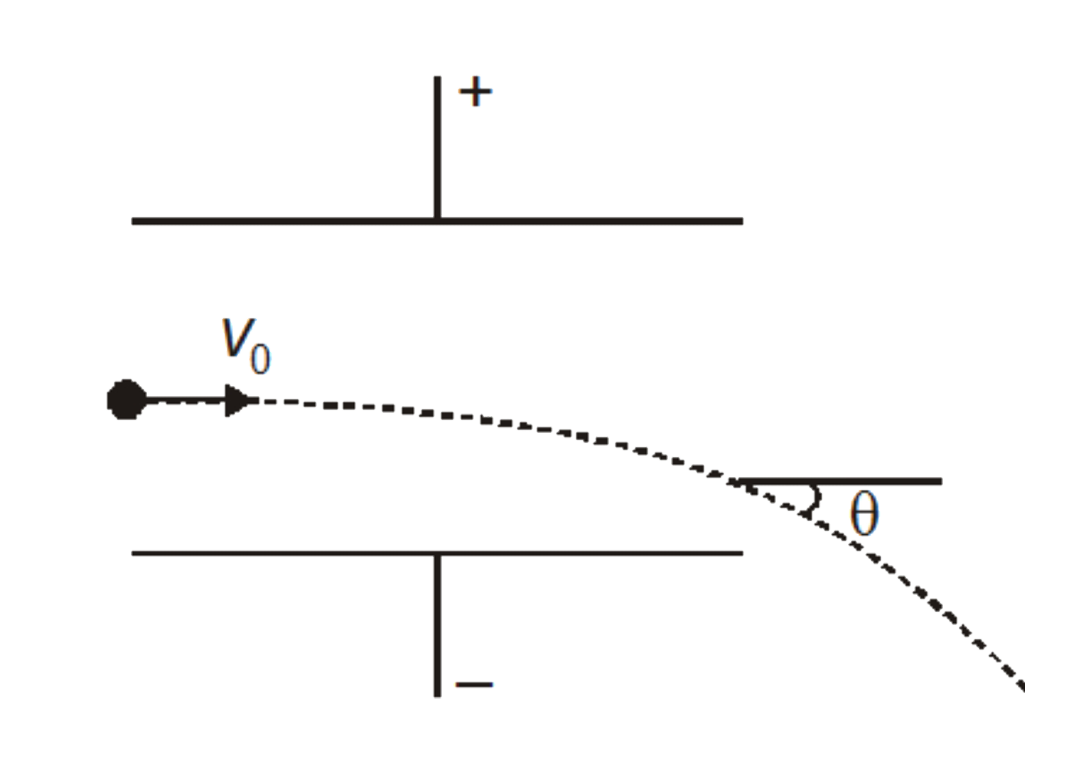
when a positively charged particle is projected with a velocity v_0 in the region between the horizontal plates of the capacitor then it leaves by making an angle theta with the horizontal , as shown. If theta=theta_1 is for proton and theta=theta_2 for an alpha - particle then the value of (tan theta_1)/(tantheta_2)
View SolutionA body is projected with a speed u at a angle theta with the horizonatl. The radius of curvature of the trajectory, when it makes an angle ((theta)/(2)) with the horizontal is (g-acceleration due to gravity)
View SolutionIf u=secθ+tanθ then tanθ in terms of u is____.
View SolutionIf u=secθ+tanθ then tanθ in terms of u is____.
View SolutionAn electron enters the region between the plates of a parallel plate capacitor at an angle θ to the plates. The plate width is l, the plate separation is d. The electron follows the path shown just missing the upper plate. Neglect gravity. Then,

View Solutionएक नति सुई प्रारंभ में चुंबकीय याम्योत्तर में स्थित होती है, जब यह एक स्थान पर नति कोण θ दर्शाती है। नति वृत्त को क्षैतिज तल में कोण से घुमाया जाता है और फिर यह नति कोण θ. दर्शाती है। तो tanθ.tanθ है:
View SolutionAn electron enters a parallel plate capacitor with horizontal speed u and is found to deflect by angle θ on leaving the capacitor as shown. It is found that an θ=0.4 and gravity is negligible

If the initial horizontal speed is doubled, then will be -
View Solutionwhen a positively charged particle is projected with a velocity v0 in the region between the horizontal plates of the capacitor then it leaves by making an angle θ with the horizontal , as shown. If θ=θ1 is for proton and θ=θ2 for an α - particle then the value of tanθ1tanθ2
View Solution
