Two small metal balls of different mass m1 and m2 are connected by strings of equal length to a fixed point. When the balls are given equal charges, the angles that the two strings make with the vertical are 30∘ and 60∘, respectively. The ratio m1/m2 is close to -
1.7
3.0
0.58
2.0
The correct Answer is:A
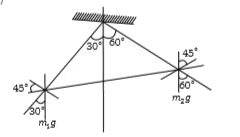
m2gsin60∘=Fcos45∘ ....(i)
m1gsin30∘=Fcos45∘ ....(ii)
On dividing eq. (i) by (ii)
m1m2=sin60sin30=√3/21/2=1.732
Similar Questions
Two equal and opposite charges of masses m1 and m2 are accelerated in an uniform electric field through the same distance. What is the ratio of their accelerations if their ratio of mass is m1m2=0.5 ?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If m_(1)=10kg, m_(2)=6kg and g =10m//s^(2) then what is the acceleration of masses?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
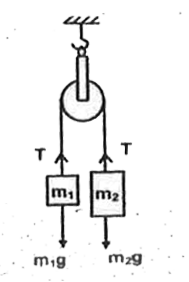
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View SolutionTwo balls of masses m_(1)=5kg, m_(2)=10kg are connected by a light inextensible string. A horizontal force F = 15 N is acting on the ball m_(2) along the line joining two balls as shown. What is the (a) acceleration of the balls (b) tension in the string?
View SolutionTwo equal and opposite charges of masses m1 and m2 are accelerated in a uniform electric field through the same distance. What is the ratio of their accelerations, if their ratio of masses is m1m2=0.5?
View SolutionTwo balls of masses m_(1)=100 g and m_(2)=300 g are suspended from point A by two equal inextensible threads, each of length l=32/35m . Ball of mass m_(1) is drawn aside and held at the same level as A but at a distance (sqrt(3)/2)l from A , as shown in Fig. When ball m_(1) is released, it collides elastically with the stationary ball of mass m_(2) . Velocity u_(1) with which the hall of mass m_(1) collides with the other ball is
View SolutionTwo balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
 The maximum rise of centre of mass of the ball of mass m2 is
The maximum rise of centre of mass of the ball of mass m2 is
View Solution
