A uniform rod is placed on two spinning wheels as shown in figure. The axes of the wheels are separated by a distance l=20cm, the coefficient of friction between that in this case the rod performs harmonic oscillations. Find the period of these oscillations.

The correct Answer is:1.5
Each roller exerts on the board forces of friction equal of f1=KN1andf2=KN2,whereN1,N2 are normals of the board on the rollers . There forces f1,f2 are shown in the figure
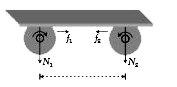
Suppose the centre of gravity of the board is slightly displaced. Let it be x from the middle . Then the forces f1,f2 will not be equal because N1andN2 will different
N1=1+xlW
When W is the weight of board and the distance between the wheel axes is l
N2=l−xl
∴f1=K(l+w)lW
and f2=K(l−x)lW
∴ Resultant force =KlW[l+x−l+x]=2KWlx
∴ Acceleration of rod =2KWxl(W/g) , since mass of rad =Wg
∴ Acceleration =2Kgxl So, acceleration is proportional to displacement . So, it executes SHM
∴ Period T=2π√l2Kg=2π√202×100×0.18×9.8=2π√12×49×0.18=1.5 sec
Similar Questions
एकसमान घनत्व वाली एक पतली छड़ एक किनारे के परिह : छोटे दोलन करती हैं। इसका आवर्तकाल T0 है। यदि दोगुनी लम्बाई की ऐसी ही छड़ को दोलन करने दे, तो आवर्तकाल होगा
View Solutionl लम्बाई की एकसमान छड़ अपने एक किनारे से लटकाई गई है और इसे छोटे दोलन दिए जाते हैं। उस सरल दोलन की लम्बाई निकालें जिसका आवर्तकाल इस छड़ के आवर्तकाल के बराबर हो।
View Solutionएक कम्पन करती हुई छड़ 2 सेकण्ड में 200 दोलन करती है। छड़ का आवर्तकाल ज्ञात कीजिए ।
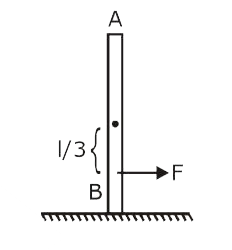
View SolutionA uniform rod ABC of mass M is placed vertically on a rough horizontal surface. The coefficient of kinetic friction between the rod and the surface is μ.A force F (>μmg) is applied on the rod at point B at distance l/3 below centre of the rod as shown in figure. The initial acceleration of point A is
View Solutionदो छड़-चुम्बकों को एक दोलन चुम्बकत्वमापी में रखा जाता है और (i) उनके समान ध्रुवों को एक ही ओर रखते हुए तथा (ii) उनके असमान ध्रुवों को एक ही ओर रखते हुए, दोलन कराये जाते हैं। वे एक मिनट में क्रमशः 20 दोलन और 15 दोलन करते हैं। इन चुम्बकों के चुम्बकीय आघूर्ण की तुलना कीजिए ।
View SolutionFind the period of small oscillations of a uniform rod with length l , pivoted at one end.
View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View Solution
