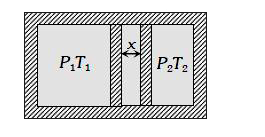
Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P1 and temperature T1 in left part and gas at pressure P2 and temperature T2 in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

P2
P1
P1(V02)γ(V02+Ax)γ
P2(V02)γ(V02+Ax)γ
The correct Answer is:C
Final volume of the left and right part
VL=V02+Ax
VR=V02−Ax
Since, container wall and piston are adiabatic in left side and gas undergoes adiabatic expansion on right side the gas undergoes adiabatic compression.
P1(V02)γ=Pγf(V02+Ax) (for left side)
P2(V02)γ=Pγf(V02−Ax) (for right side)
∴P1P2=(V02+Ax)γ(V02−Ax)γ⇒Ax=V02[P1/γ1−P1/γ2][P1/γ1+P1/γ2]
Now, Pf=P1(V02)γ[V02+Ax]γ
Similar Questions
A heat conducting piston can move freely inside a closed thermally isolated cylinder which contains an ideal gas. In equilibrium the piston divides the cylinder in two equal parts, the temperature of the gas being T_(0) . The piston is slowly displaced. Find the temperature of the gas when the volume of one part is n times greater than that of the other part. The adiabatic exponent of the gas is gamma .
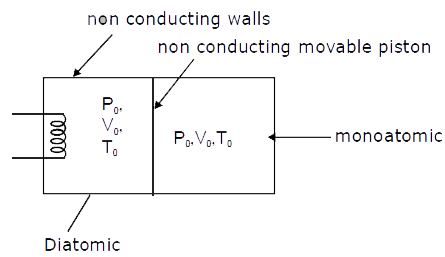
View SolutionA cylindrical container having nonconducting walls is partitioned in two equal parts such that the volume of the each parts is equal toV0. A movable nonconducting piston is kept between the two parts. Gas on left is slowly heated so that the gas on right is compressed upto volume V08. Find pressure and temperature on both sides if initial pressure and temperature, were P0andT0 respectively. Also find heat given by the heater to the gas. (number of moles in each part is n)
View SolutionA cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
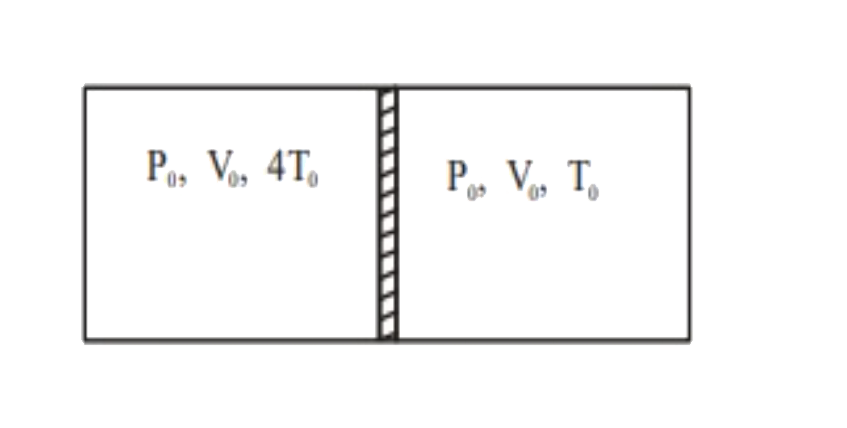
View SolutionA piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5V and the other part has pressure 8P and volume V, the piston is now left free. Find the new pressure and volume for the isothermal and adiabatic process. (γ = 1.5).
View SolutionA piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5Vand the other part has pressure 8P and volume V, the piston is now left free. Find the new pressure and volume for the isothermal and adiabatic process.
View SolutionA piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5V and the other part has pressure 8P and volume V, the piston is now left free. Find the new pressure and volume for the isothermal and adiabatic process. (γ=1.5).
View SolutionFigure shows an adiabatic cylindrical tube of volume (V_0) divided in two parts by a frictionless adiabatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (P_1) and the temperatures (T_1) is injected into the left part and the another ideal gas at pressures (P_2) and temperature (T_2) is injected into the right part. (C_p / C_v = gamma) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.
View SolutionFollowing figure shows on adiabatic cylindrical container of volume V_(0) divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (C_(p)//C_(y)=lambda) is at pressure P_1 and temperature T_1 in left part and gas at pressure P_2 and temperature T_2 in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
View Solution
