Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
12π√d33Gm
2π√d33Gm
2π√3Gmd3
12π√3Gmd3
The correct Answer is:B
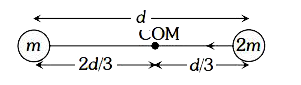
F=G(2m)md2=(2m)ω2(d/3)
Gmd2=ω2d3⇒ω2=3Gmd3
⇒ω=√3Gmd3
⇒T=2πω=2π√d33Gm
Similar Questions
In a double star system two stars of masses m1 and m2 seperated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionA double star is a system of two stars rotating about their centre of mass only under their mutual gravitational attraction. Let the stars have masses m and 2m and let their separation be 1. Their time period of rotation about their centre of mass will be proportional to (a) 1^(3//2) , (b)a , (c) m ,(d) m^(-1//2)
View SolutionIn a double star system, two stars of masses m_(1) and m_2 seperated by a distance d rotate about their centre of mass. Then their common angular velocity would be:
View SolutionIn a double star system two stars of masses m1andm2 separated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionA double star is a system of two stars rotating about their centre of mass only under their mutual gravitational attraction. Let the stars have masses m and 2m and let their separation be 1. Their time period of rotation about their centre of mass will be proportional to a) 1^(3//2) b) a c) m d) m^(-1//2)
View SolutionIn a double star system two stars of masses m1 and m2 separated by a distance 'd' rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionIn a double star system two stars of masses m1 and m2 separated by a distance 'd' rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View Solution

