A satellite of mass m is launched vertically upwards with an initial speed u from the surface of the earth. After it reaches height R(R = radius of the earth), it ejects a rocket of mass so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is (G is the gravitational constant, M is the mass of the earth)
The correct Answer is:B
By conservation of energy
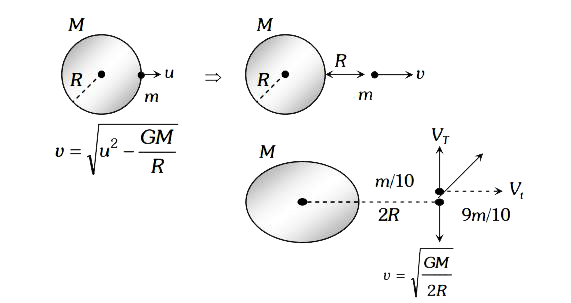
Kinetic energy
Similar Questions
एक उपग्रह जिसका द्रव्यमान m है, पृथ्वी के चारों ओर पृथ्वी की सतह से ऊँचाई R पर चक्कर लगा रहा है | यदि पृथ्वी की सतह पर गुरुत्वीय क्षेत्र की तीव्रता g है और पृथ्वी की त्रिज्या R है, तो उपग्रह की गतिज ऊर्जा होगी :
View SolutionA satellite of mass 'M' is projected radially from surface of earth with speed 'u'. When is reaches a height equal to radius of earth, it ejects a rocket of mass ( M)/(10 ) and it itself starts orbiting the earth in circular path of radius 2R, find the kinetic energy of rocket.
View Solutiona satellite moving with a constant speed V in a circular orbit about the earth an object of mass m is ejected from the satellite such that it just escapes from the gravitational pull of the earth at the time of its ejection the kinetic energy of the object is
View SolutionA satellite of mass m is launched vertically upwards with an initial speed sqrt((GM)/®) from the surface of the earth. After it reaches height R (R = radius of the earth), it ejects a rocket of mass m/10 in a direction opposite to the initial direction of the satellite, so that subsequently the satellite escapes to infinity. The minimum kinetic energy of the rocket at ejection needed is (G is the gravitational constant, M is the mass of the earth):
View SolutionA satellite of mass m is launched vertically upwards with an initial speed U from the surface of the Earth. After it reaches height 2 R (R = radius of Earth) it ejects a rocket of mass (m)/(5) So, that subsequently the satellite moves in a circular orbit. The kinetic energy of rocket is (M is mass of Earth)
View SolutionA satellite of mass m is launched vertically upwards with initial kinetic energy K from the Earth’s surface. After it reaches height R (R = radius of earth). It ejects a rocket of mass m5 so that subsequently the satellite moves in a circular orbit. The kinetic energy of rocket is [G is gravitational constant, M is the mass of the earth, take GMmR=K]
View SolutionAn artificial satellite of mass m orbits earth at a height R above the surface of earth. If g denotes gravitational field intensity at the surface of earth of radius, R, the kinetic energy f the revolving satellite will be
View SolutionA rocket mass M is launched vertically from the surface of the earth with an initial speed V. Assuming the radius of the earth to be R and negligible air resistance, the maximum height attained by the rocket above the surface of the earth is
View Solution
