particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
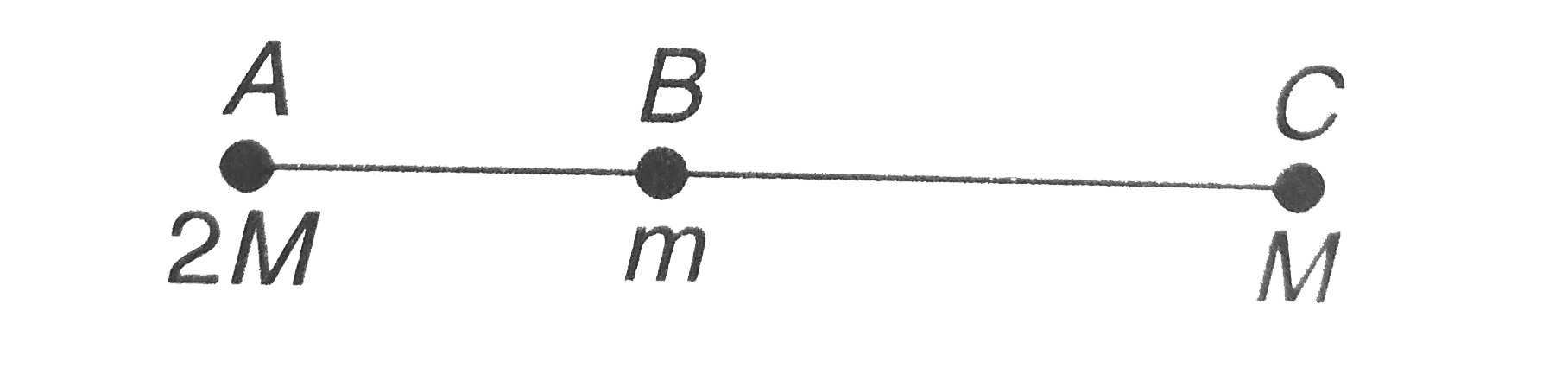
m will remain at rest
m will move towards M
m will move towards 2M
m will have oscillatory motion
The correct Answer is:C
Force on B due to A=FBA=G(2Mm)(AB)2 towards BA
Force on B due to C=FBC=GMm(BC)2 towards BC
As, (BC)=2AB
⇒FBC=GMm(2AB)2=GMm4(AB)2<FBA
Hence, m will move towards BA (i.e., 2M )
Similar Questions
कणों के द्रव्यमान 2M, m एवं M क्रमश: बिन्दुओं A, B एवं Cपर AB = 1/2 (BC) के साथ हैं। m, M से बहुत छोटा है एवं समय t=0 पर, वे सभी विरामावस्था में हैं। किसी भी टक्कर के होने रो गूर्व क्रागिक

View Solutionparticles of masses 2M m and M are resectively at points A , B and C with AB = (1)/(2) (BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
View Solutionparticles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .

View Solution2M,m तथा M द्रव्यमान के कण क्रमश: A,B तथा C बिन्दुओं पर इस प्रकार स्थित हैं कि AB=1/2(BC) है तथा M की तुलना में m बहुत छोटा है और समय t=0 पर ये सभी विराम में हैं (चित्र में) तदान्तर, किसी संघटट से पूर्व

View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v_(0) in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest (a). Find the ratio m//M (b). A point P on the rod is at rest immediately after collision find the distance AP. (c). Fid the linear speed of the point P a time piL//3v_(0) after the collision.
View SolutionParticles of masses 2M, m and M are respectively at points A, B and C with sqrt((GM)/(R))(sqrt(2)+1) is much-much smaller than M and at time t=0 , they are all at rest as given in figure At subsequent time before any collision takes place.
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v_(0) in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest (a). Find the ratio m//M (b). A point P on the rod is at rest immediately after collision find the distance AP. (c). Find the linear speed of the point P a time piL//3v_(0) after the collision.
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v_(0) . Answer the following three questions regarding this collision. Minimum kinetic energy of the particle after collision is
View Solution