Particle A of mass $m_{A} = \frac{m}{2}$ moving along the x - axis with velocity $v_{0}$ collides elastically with another particle B at rest having mass $m_{B} = \frac{m}{3}$ . If both particles move along the x - axis after the collision , the change $Δ λ$ in de - Broglie wavelength of particle A , in terms of its de - Broglie wavelength $(λ_{0})$ before collision is :

A

$Δ λ = \frac{3}{2} λ_{0}$

B

$Δ λ = \frac{5}{2} λ_{0}$

C

$Δ λ = 2 λ_{0}$

D

$Δ λ = 4 λ_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

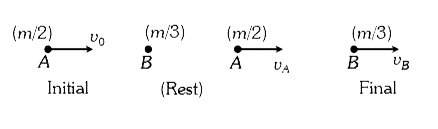
Applying momentum conservation $\frac{m}{2} \times v_{0} + \frac{m}{3} \times (0) = \frac{m}{2} v_{A} + \frac{m}{3} v_{B}$
$= \frac{v_{0}}{2} = \frac{v_{A}}{2} + \frac{v_{B}}{3}$ ...(i)
Since, collsion is elastic (e=1)
$e = 1 = \frac{v_{B} - v_{A}}{v_{0}} \Rightarrow v_{0} = v_{B} - v_{A}$ ...(ii)
on solving eq (i) & (ii): $v_{A} = \frac{v_{0}}{5}$
Now, de-Broglie wavelength of A before collision: $λ_{0} = \frac{h}{m_{A} v_{0}} = \frac{h}{(\frac{m}{2}) v_{0}}$
$\Rightarrow λ_{0} = \frac{2 h}{m v_{0}}$
Final De-Broglie wavelength
$λ_{f} = \frac{h}{m_{A} v_{0}} = \frac{h}{\frac{m}{2} \times \frac{v_{0}}{5}} \Rightarrow λ_{f} = \frac{10 h}{m v_{0}}$
Now, $Δ λ = λ_{f} - λ_{0}$
$Δ λ = \frac{10 h}{m v_{0}} - \frac{2 h}{m v_{0}}$
$\Rightarrow Δ λ = \frac{8 h}{m v_{0}} \Rightarrow Δ λ = 4 \times \frac{2 h}{m v_{0}}$
$\Rightarrow Δ λ = 4 λ_{0}$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile