A particle A of mass m and initial velocity v collides with a particle of mass $m / 2$ which is at rest. The collision is head on, and elastic. The ratio of the de-broglie wavelength $λ_{A} and λ_{B}$ after the collision is

A

$\frac{λ_{A}}{λ_{B}} = \frac{1}{2}$

B

$\frac{λ_{A}}{λ_{B}} = \frac{1}{3}$

C

$\frac{λ_{A}}{λ_{B}} = 2$

D

$\frac{λ_{A}}{λ_{B}} = \frac{2}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

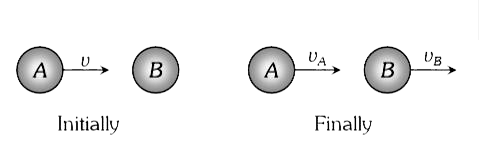
momentum Conservation
$m v = m v_{A} + \frac{m}{2} v_{B}$ ...(i)
$e = \frac{v_{B} - v_{A}}{v} = 1$ ...(ii)
$2 (v_{B} - v_{A}) = 2 v_{A} + v_{B}$
$2 v_{B} - v_{B} = 4 v_{A}$
$v_{B} = 4 v_{A}$
$\frac{λ_{A}}{λ_{B}} = \frac{m_{B} v_{B}}{m_{A} v_{A}} = \frac{m / 2}{m} \times 4 = 2$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile