Consider a rubber ball freely falling from a height h = 4.9 m on a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:
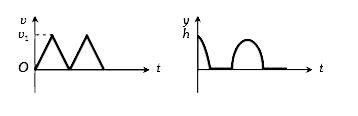

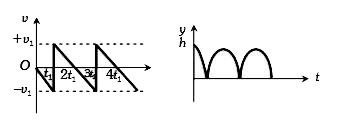
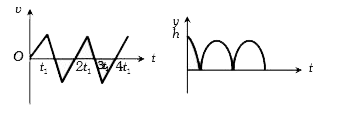
The correct Answer is:C
Velocity of ball gets several at highest point
Similar Questions
A ball falls freely on a perfectly elastic plate from a height of 3m . At the instant t = 0 , the velocity of the ball is zero. Draw velocity -time graph for the motion of the ball. [g = 9.8 m.s−2 ]
View SolutionConsider a rubber ball freely falling from a height h = 4.9 m on to a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be :
View SolutionConsider a rubber ball freely falling from a height h = 4.9 m onto a horizontally elastic plate. Assume that the duration of collision is negligible and the collisions with the plate is totally elastic . Then the velocity as a function of time and the height as a function of time will be :
View SolutionA rubber ball dropped from a height of 20 cm (g = 10 m//s^(2)) falls on the roof of an elevator going up at 2 m/s. If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of
View SolutionA rubber ball dropped from a height of 20m (g= 10 m//s^(2)) falls on the roof of an elevator going up at 2m/s. If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of
View SolutionConsider a rubber ball falling from h = 4.9 m height on a horizontal elastic plate. Suppose the duration of the collision is negligible and the collision with the plate is completely elastic. Then the velocity as the function of time and the height as the function of time will be -
View SolutionA stone is projected from a horizontal plane. It attains maximum height H & strikes a stationary smooth wall & falls on the ground vertically below the maximum height. Assuming the collision to be elastic the height of the point on the wall where ball will strike is
View SolutionAn elastic ball of mass m falls from a height h on an Aluminium disc of area A floating in a mercury pool. If the collision is perfectly elastic, the momentum transferred to the disc is :
View Solution

