A ball of mass m suspended from a rigid support by an inextensible massless string is released from a height h above its lowest point. At its lowest point it collides elastically with a block of mass 2m at rest on a frictionless surface. Neglect the dimensions of the ball and the block. After the collision the ball rises to a maximum height of–

h3
h2
h8
h9
The correct Answer is:D
As mgh=12mv2
⇒v=√2gh , velocity of ball before collision
Using law of conservation of momentum
mv=mv1+2mv2
⇒v1+2v2=v ...(i)
v1andv2 are velocity of ball and block after collision as coefficient of restitution (e)
e=v2−v1v−0
⇒v2−v1=v ...(iii) [ as e = 1 ]
From (i) + (ii)
v2=v3andv1=v3
Hence, after collision maximum height
Hmax=v212g=⎛⎜
⎜
⎜
⎜⎝(√2gh3)2g⎞⎟
⎟
⎟
⎟⎠2
Hmax=h9
Similar Questions
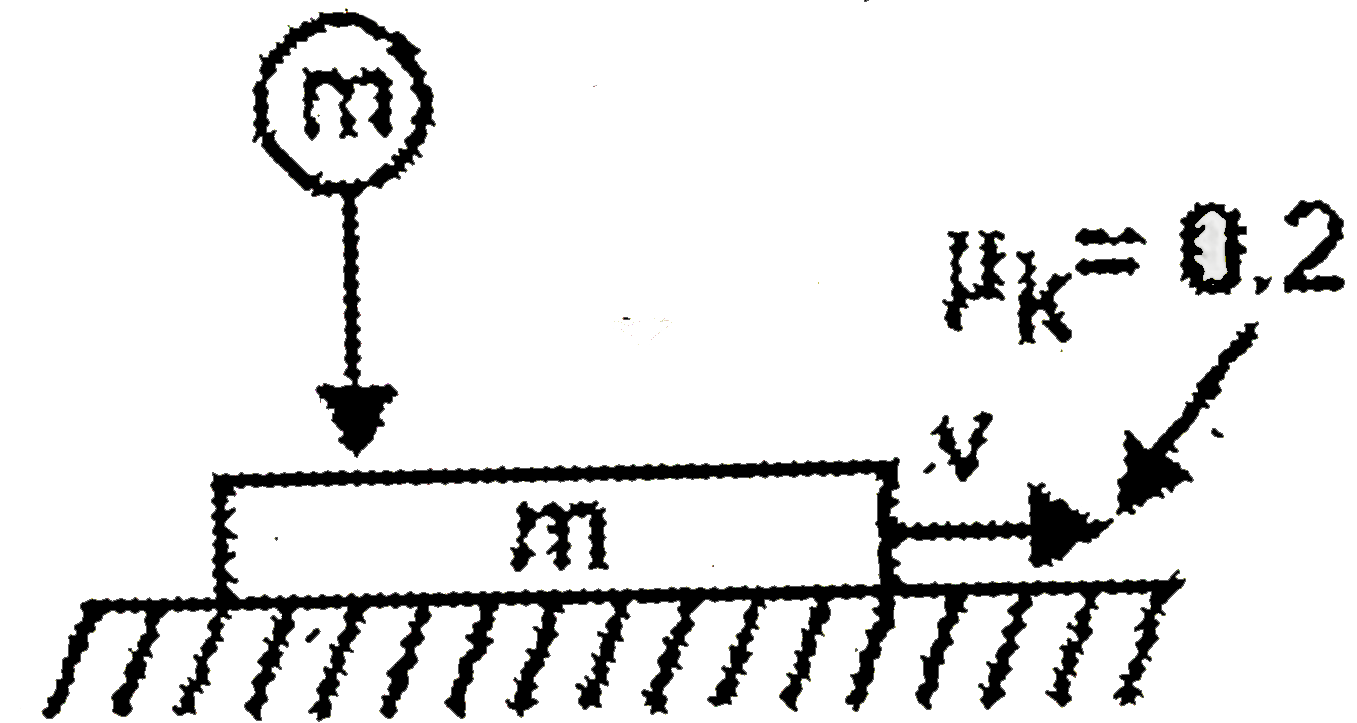
A ball of mass m falls vertically from a height h and collides with a block of equal mass m moving horizontally with a velecity υ on a surface. The coefficient of kinetic friction between the block and the surface is 0.2, while the coefficient of restitution e between the ball and the block is 0.5. There is no friction acting between the ball and the block. The velocity of the blockdecreases by :
View SolutionTwo pendulum bobs of masses m and 2m collide elastically at the lowest point in their motion, when the centres are at the same level as shown in the figure. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision ?
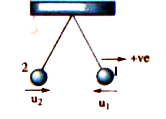
View SolutionTwo pendulum bobs of mass m and 2m are attached to treads of lengths L suspended from a rigid support. Boty the bobs are taken to a height H from the lowest point and then released so they collide elastically at the lowest point in their motion. Velocity of bob of mass m just after impact is
View SolutionA tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
View SolutionTwo pendulum bobs of masses m and 2m collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
View SolutionA spherical rigid ball is realeased from rest and starts rolling down an inclined plane from height h=7m, as shown in the figure. It hits a block at rest on the horizontal plane (assme elastic collision). If the mass of both the ball and the block is m and the ball is rolling without sliding, then the speed of the block after collision is close to
View SolutionA small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M=4m. They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.

View SolutionA tennis ball is thrown from a height h above the ground. If the ball strikes to the ground with elastic collision, what height will the ball achieve after the third collision?
View Solution