mass of 0.5 kg moving with a speed of on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be
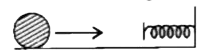
0.15 m
0.12 m
1.5 m
0.5 m
The correct Answer is:A
Similar Questions
m द्रव्यमान का एक गुटका v चाल से क्षैतिज खुरदुरी सतह पर गतिमान है तथा चित्रानुसार स्प्रिंग नियतांक k वाली क्षैतिज रूप से व्यवस्थित स्प्रिंग से टकराता है। गुटके एवं फर्श के मध्य का घर्षण गुणांकμ है। स्प्रिंग का अधिकतम संपीड़न होगा-

View SolutionA body of 0.5 kg mass runs 1.5 m / s on a friction-free horizontal plane, which almost collides with the weight spring. The force of the spring is constant k = 5ON / m. The maximum compression distance of the spring will be:
View SolutionA mass of 0.5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with string of force constant 50 N/m . How much maximum compression on the spring will be ?
View SolutionA car of mass 1000 kg moving with a speed 18 km h^(-1) on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25 xx10^3 N m^(-1) . The maximum compression of the spring is
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA mass of 0.5 kg moving with a speed of 1.5 m//s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k =50 N//m The maximum compression of the spring would be.
View SolutionA block of mass m moving with velocity v_(0) on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
View SolutionA mass of 0.5 kg mass on a smooth horizontal surface 1.5 m//s A forceless and at the speed of no K = 50 N//m If the force-constant collides with the spring, find the maximum compression of the spring.
View Solution