The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

The correct Answer is:15
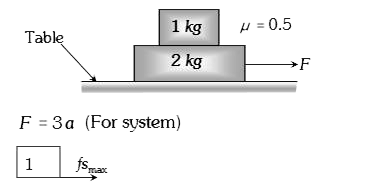
fmax=1a (for 1kg block)
μ×1×g=a
⇒5=a
F=15N
Similar Questions
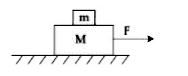
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2. If a horizontal force of 50 N is applied on the block, the frictional force is
View SolutionOn a smooth table two blocks of masses 2.5 kg and 1.5 kg are placed one over the other as shown in figure. If the coefficient of static friction between two blocks is 0.2, the maximum horizontal force to be applied on the lower block so that the two blocks move together is (g=ms−2)
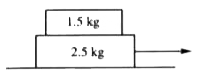
View SolutionTwo blocks ( m = 0.5 kg and M = 4.5 kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is 37. Then the maximum horizontal force that can be applied on the larger block move together is _____________ N. ( Round off to the Nearest Integer ) [Take as 9.8ms−2 ]
View SolutionA 3 kg block is placed over a 10 kg block and both are palced on a smooth horizontal surface. The coefficient of friction between the block is 0.2 . If a horizontal force of 20 N is applied to 3 kg block, accelerations of the two block in ms−2 are (take, g=ms−2)

View SolutionOn smooth horizontal surface a block A of mass 10 kg is kept . On this block a second block B of mass 5 kg is kept .The coefficient of friction between the two blocks is 0.4 .A horizontal force of 30 N is applied on the lower block as shown . The force of friction between the blocks is (take g = 10 m//s^(2) )
View SolutionA block is at rest on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the floor is 0.8. If the force of friction on the block is 10 N, then the mass of the block is: ( g = 10 ms^(-2) Take)
View Solution

