What is the maximum value of the force F such that the block shown in the arrangement, does not move ?
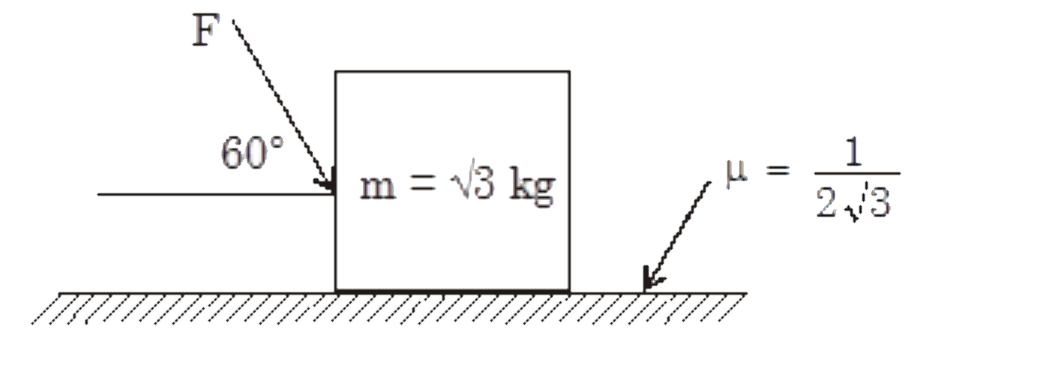
20N
10N
12N
15N
The correct Answer is:A

.
Similar Questions
What is the maximum value of the force F (in newton) such that the block shown in the arrangement, does not move ?
View SolutionThe maximum value of the applied force F such that the block as shown in the arrangement does not move is (Acceleration due to gravity, g=10 ms^-2 )
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move?
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move?
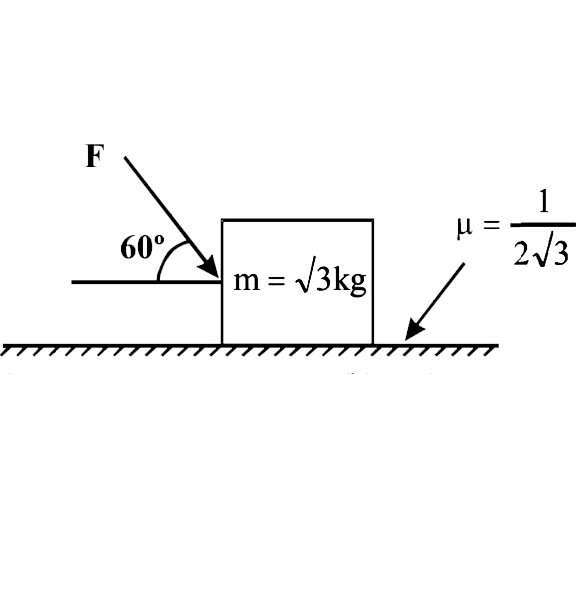
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement does not move ?
(Given μ=12√3

View SolutionWhat is the maximum value of the force F such that the block shown in the figure does not move?
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move:
View SolutionFor the arrangement as shown in the figure the maximum force F, for no relative motion between blocks is
View Solution