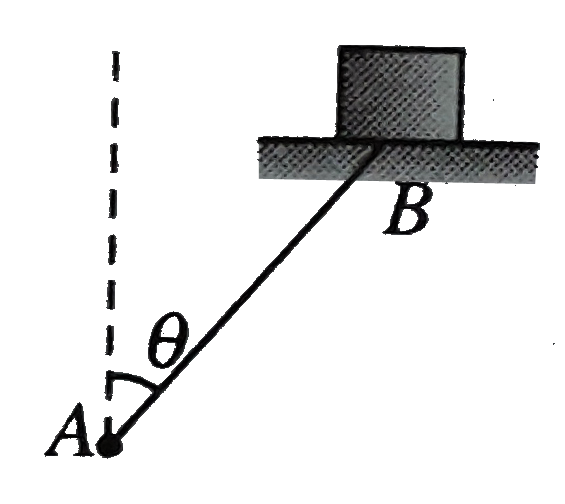
A rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
The correct Answer is:1
N=mg,μN=mrω2

μmg=m2sinθω2
⇒ω=√μg2sinθ=√0.1×102×sin30=1rads−1
Similar Questions
A block is placed on a horizontal platform. The system is making horizontal oscillations about a fixed point with a frequency of 0.5 Hz. The maximum amplitude of oscillation if the block is not to side on the horizontal platform, is (Coefficient of friction between the block and the platform = 0.4)
View SolutionA block is placed on a horizontal platform. The system is making horizontal oscillations about a fixed point with a frequency of 0.5Hz. The maximum amplitude of oscillation if the block is not to slide on the horizontal platform, is (Coefficient of friction between the block and the platform = 0.4)
View SolutionA uniform rod AB of mass m is hinged at one A. The rod is kept in horizontal position by a massless string tied to point B. The reaction of the hinge on the end A of the rod at the instant, when string is cut is mg/x. Where 'x' is

View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)

View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle theta = 30^(@) with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is mu = 0.1 then find the maximum angular velocity in rad s^(-1) of rod so that the block does not slip on the plateform (g = 10 ms^(-2))
View Solution
