A ball after having fallen from rest under the influence of gravity for 6 s crashes through a horizontal glass plate, thereby losing two-third of its velocity. It then reaches the ground in 2 s, find the height of the plate above the ground.
The correct Answer is:58.8
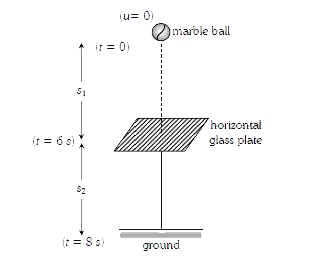
v=u+at=0+g×6 ∴V=6g
s1=12g×36=2g
When marble ball crashes through horizontal glass plate then velocity after crash is
6g−6g×23=2g
Distance for remaining 2 seconds
∴S2=2g×2+12g×4
=4g+2g=6g=6×9.8
= 58.8 m .
Similar Questions
A body released from rest to fall freely under gravity reaches the ground in 4 s. Then the height from which it is released is
View SolutionA ball projected upwards from the foot of a tower. The ball crosses the top of the tower twice after an interval of 6 s and the ball reaches the ground after 12 s . The height of the tower is (g = 10 m//s^2) :
View SolutionA ball falls under gravity from a height of 10m with an initial velocity. It collides with the ground,loses 50% of its engery and then rises to the same height.Find the initial velocity.
View SolutionA ball is released from a height and it reaches the ground in 3 s. If g=9.8m s−2, find the value of the height from which the ball was released.
View SolutionA ball is released from a height and it reaches the ground in 3 s. If g=9.8 "m s"^(-2) , find the value of the velocity with which the ball will strike the ground.
View SolutionA body falls freely under gravity from rest and reaches the ground in time t. Write an expression for the height fallen by the body.
View SolutionA man in a balloon, rising vertically with an acceleration of 5m/s2, releases a ball 10 s after the balloon is let go from the ground. The greatest height above the ground reached by the ball is
View SolutionA ball after having fallen from rest under the influence of gravity for 6 s crashes through a horizontal glass plate, thereby losing two-third of its velocity. It then reaches the ground in 2 s, find the height of the plate above the ground.
View Solution
