Three blocks , of masses m1=2.0,m2=4.0 and m3=6.0kg are connected by strings on a frictionless inclined plane of 60∘ , as shown in the figure. A force F=120N is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The values of tensions T1 and T2 in the cords are.
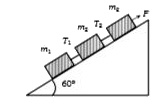
T1=20N,T2=60N
T1=60N,T2=60N
T1=30N,T2=50N
T1=20N,T2=100N
The correct Answer is:A
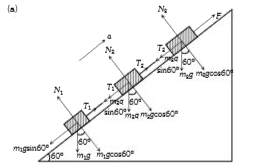
Here
m1=2.0kg,m2=4.0kg,m3=6.0kgF=120N
Let a be common acceleration of the system.
The equation of motion of block 1 is
T1−m1gsin60∘=m1a …….(i)
The equation of motion of block 2 is
T2−T1−m2gsin60∘=m2a ............(ii)
The equation of motion of block 3 is
F−T2−m3gsin60∘=m3a ..........(iii)
Adding (i), (ii) and (iii) , we get
F−(m1+m2+m3)gsin60∘=(m1+m2+m3)a
a=F−(m1+m2+m3)gsin60∘m1+m2+m3
=120N−(2kg+4kg+6kg)(9.8m/s∘)(0.866)2kg+4kg+6kg
=120−(12kg)(9.8m/s2)(0.866)12kg=1.51m/s2
From equation (i) ,
T1=m1gsin60∘+m2a=(2kg)(9.8m/s2)(0.86)+(2kg)(1.51m/s2)
=20N
From equation (iii) ,
T2=F−m3gsin60∘−m3a=120−(6kg)(9.8m/s2)(0.866)−(6kg)(1.51m/s2)
= 60 N.
Similar Questions
Three blocks of masses m_(1), m_(2) and m_(3) are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force T_(3) = 40N . If m_(1) = 10kg, m_(2) = 6kg and m_(3) = 4kg , then tension T_(2) will be
View SolutionConsider three blocks of masses m_(1), m_(2), m_(3) interconnected by strings which are pulled by a common force F on a frictionless horizontal table as in the figure. The tension T_(1) and T_(2) are also indicated a) T_(2) gt T_(1)" if "m_(2) gt m_(1) b) T_(2) =T_(1)" if "m_(2)=m_(1) c) T_(2) gt T_(1) always d) "acceleration of the system"=(F)/(m_(1)+m_(2)+m_(3))
View SolutionAs in the diagram three blocks connected together lie on a horizontal frictionless table and pulled to the right with a force F=50 N if m1=5kgm2=10 kg and m3=15kg find the tensions T1 and T2
View SolutionShown in the picture m_(1)=2.0, m_(2)=4.0 And m_(3)=6.0 kg Three blocks of a plane 60^(@) The frictionless chute is connected by a rope on the plane, if the rope is light then the tension on the rope T_(1) And T_(2) will be honoured
View SolutionThere blocks of masses m1,m2 and m3 are connected by massless strings as shown in figure on a frictionless table. They are pulled with a force T3=50 N. If m1=10 kg, m2=6 kg and m3=2 kg, the tension T2 will be

View SolutionThree blocks of masses m1,m2and m3 are connected by massless strings as shown on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kg and m3=4kg the tension T2 will be

View SolutionTwo blocks A and B are connected by a string as shown as shown in the figure . Friction coefficient of the inclined plane is 0.5 . The mass of the block A is 5 kg. If minimum and maximum values of mass of the block B for which the block A remains in equilibrium are m_(1) and m_(2) then find the value of (m_(2) - m_(1)) [in kg]
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
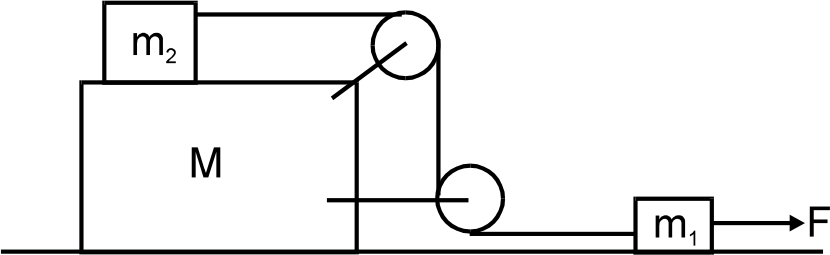
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View Solution