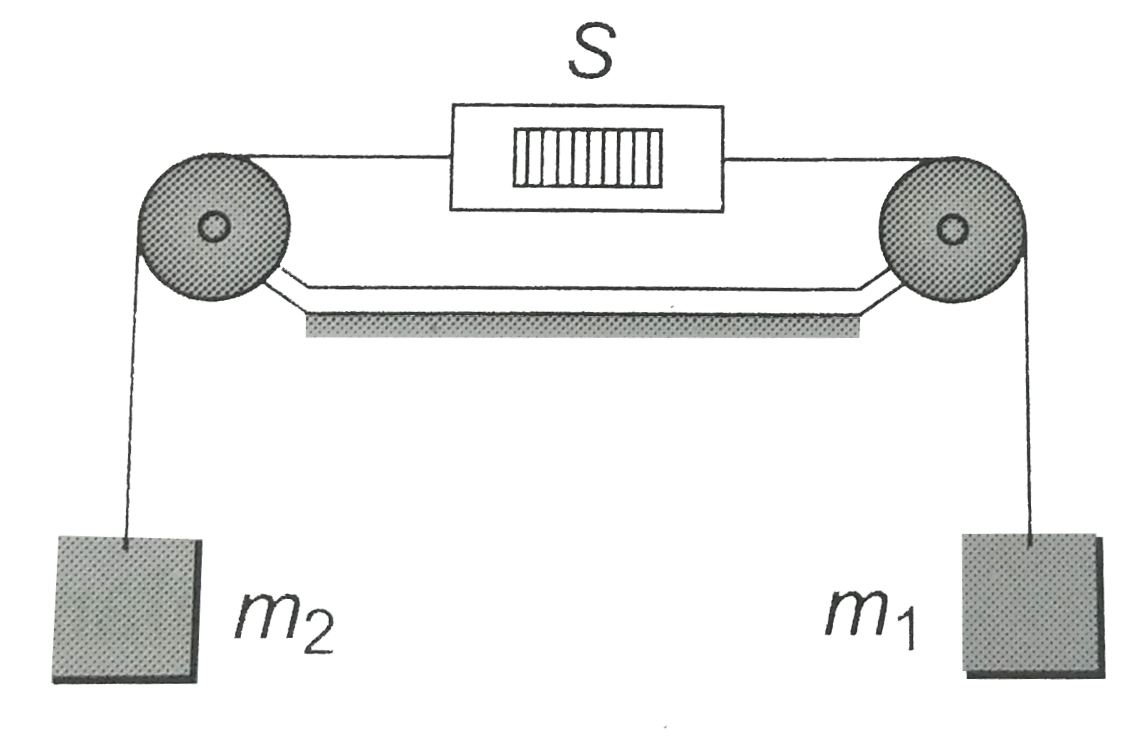
In the arrangement shown, the pulleys are fixed and ideal, the strings are light, m1>m2 and S is a spring balance which is itself massless. The readings of S (in units of mass) is
m1−m2
12(m1+m2)
m1m2m1+m2
2m1m2m1+m2
The correct Answer is:D
Reading of spring balance = T
T=2m1m2m1+m2gN
Mass =2m1m2m1+m2
Similar Questions
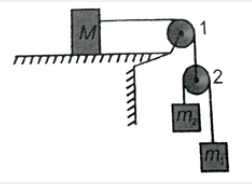
In the arrangment as shown below m1=1kg,m2=2kg . Pulleys are massless and strings are light . For what value of M the mass m1 moves with constant velocity . ( Neglect Friction)
View SolutionIn the arrangement shown, the pulleys, string and the spring balance, all the ideal. If m_(1) gt m_(2) , then the reading of the spring balance is
View SolutionPulleys are ideal and string are massless. The masses of blocks are m_(1) = 4kg and m_(2) = 1kg as shown.If all surfaces are smooth then the acceleration of m_(2) in m//s^(2) is ( g =10 m//s^(2) )
View SolutionThree blocks of masses m_(1)=4kg, m_(2)=2kg, m_(3)=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m//s^(2))
View SolutionTwo masses m_(1) and m_(2) are attached to a spring balance S as shown in Figure. If m_(1)gt m_(2) then the reading of spring balance will be
View SolutionIn the arrangement shown in figure pulleys and strings are ideal m1>m2. S is spring balance which is itself massless. The reading of balance will be

View SolutionIn the arrangement shown in fig. m1=1kg,m2=2kg. Pulleys are massless and strings are light. For what value of M, the mass m1 moves with constant velocity.

View SolutionIn the arrangment as shown below m_(1) = 1 kg, m_(2) = 2 kg . Pulleys are massless and strings are light . For what value of M the mass m_(1) moves with constant velocity . ( Neglect Friction)
View Solution