Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
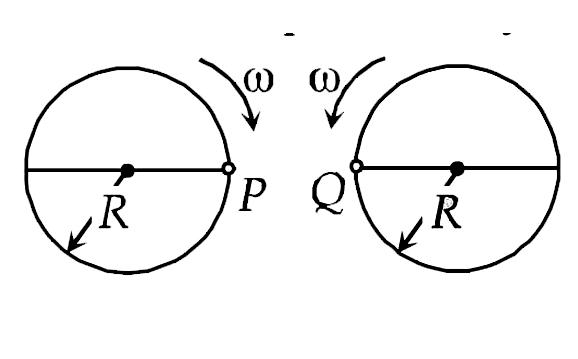




The correct Answer is:A
In each rotation relative speed becomes zero twice and becomes maximum twice
Aliter : At t = 0 the relative velocity will be maximum in magnitude
At t=T2 the relative velocity will be zero
At t=3T2 the relative velocity will be maximum in magnitude
At t = T the relative velocity again become zero
Similar Questions
Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed omega . The discs are in the same horizontal plane. At time t-0, the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is v_r , As a function of time, it is best represented by
View SolutionA cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed omega=(v)/(R) in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
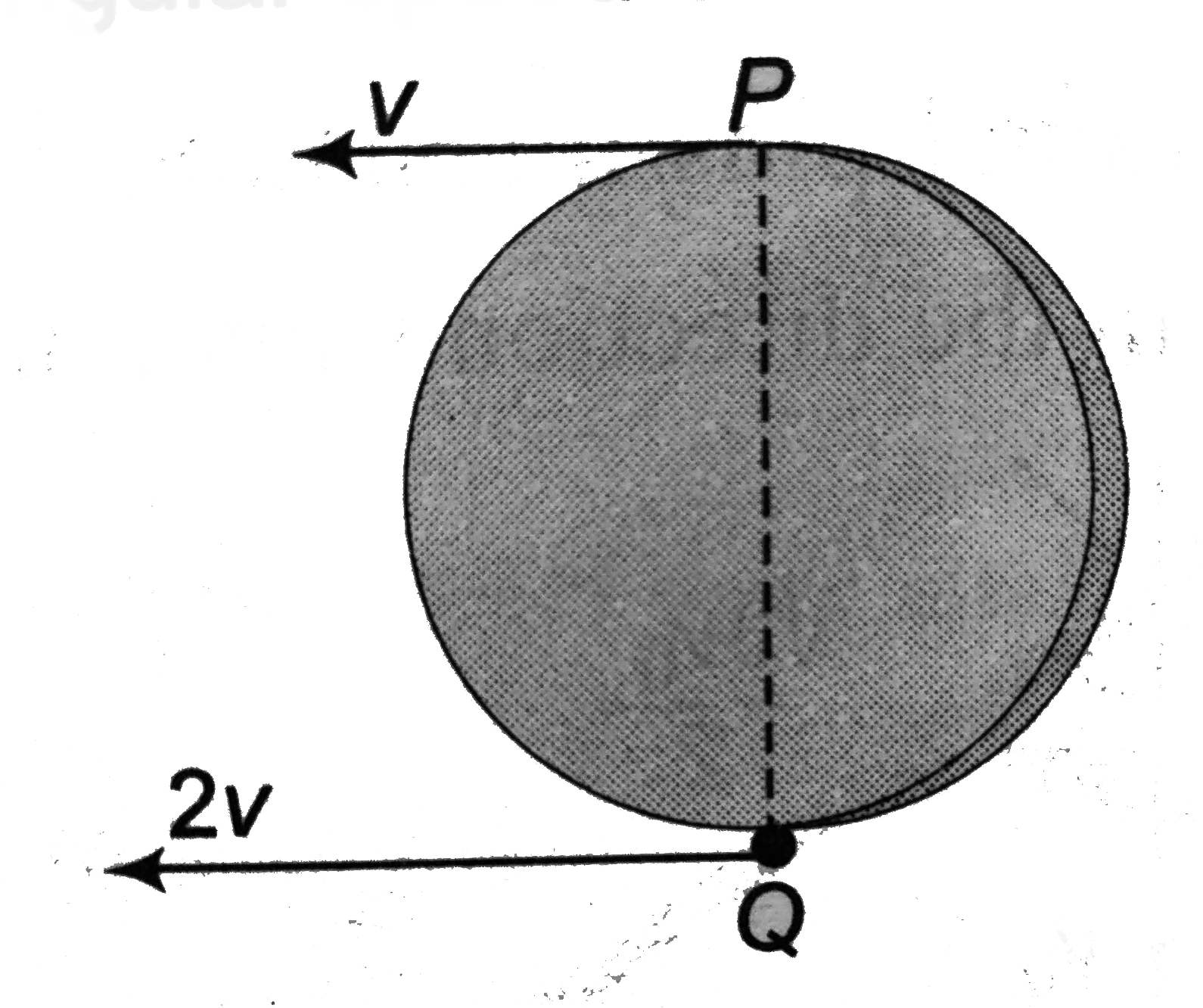
View SolutionTwo point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed omega about its center O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 1//8 rotation, (ii) their range is less than half the disc radius, and (iii) omega remains constant throughout. Then
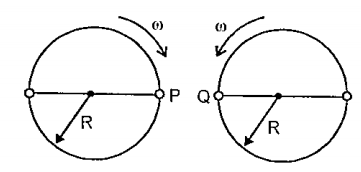
View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed omega . The discs are in the same horizontal plane. At time t = 0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is v_(r) . In one time period (T) of rotation of the discs , v_(r) as a function of time is best represented by
View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t = 0, the points P and Q are facing each other as shown in the figure. The relative speed between the two points. P and Q is vr As a function of time, it is best represented by
View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed omega about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed (1)/(8) rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
View SolutionA disc of mass M and radius R is rolling with angular speed omega on a horizontal plane as shown in figure. The magnitude of angular momentum of the disc about the origin O is
View Solution