Match List - I with List – II
List - IList - II(A) Magnetic Induction(ii)ML2T−2A−1(B) Magnetic Flux(ii)M0L−1A(C) Magnetic permeability(iii)MT−2A−1(D) Magnetization (iv)MLT−2A−2
Choose the most appropriate answer from the options given below
(A)-(iii), (B)-(ii), (C)-(iv), (D)-(i)
(A)-(iii), (B)-(i), (C)-(iv), (D)-(ii)
(A)-(ii), (B)-(iv), (C)-(i), (D)-(iii)
(A)-(ii), (B)-(i), (C)-(iv), (D)-(iii)
The correct Answer is:B
To solve the problem of matching List - I with List - II, we will derive the dimensional formulas for each of the magnetic quantities in List - I and then match them with their corresponding formulas in List - II.
1. Magnetic Induction (B):
- The formula for the magnetic induction B can be derived from the force on a current-carrying wire in a magnetic field:
F=I⋅L⋅B
- Rearranging gives:
B=FI⋅L
- The dimensions of force F are MLT−2, current I has dimensions A, and length L has dimensions L.
- Therefore, substituting these into the equation gives:
B=MLT−2A⋅L=MT−2A
- Thus, the dimensional formula for magnetic induction B is:
(B)=MT−2A−1
- This matches with option (iii) in List - II.
2. Magnetic Flux (Φ):
- The formula for magnetic flux Φ is given by:
Φ=B⋅S
- Where S is the area. The dimensions of area S are L2.
- Substituting the dimensions of B:
Φ=(MT−2A−1)⋅(L2)=ML2T−2A−1
- Thus, the dimensional formula for magnetic flux Φ is:
(Φ)=ML2T−2A−1
- This matches with option (i) in List - II.
3. Magnetic Permeability (μ):
- The magnetic permeability μ is defined as:
μ=BH
- We already have B and need to find H (magnetic field strength). The dimensions of H are:
H=Bμ
- The dimensions of H are AL−1.
- Substituting the dimensions of B:
μ=MT−2A−1AL−1=MT−2A2
- Thus, the dimensional formula for magnetic permeability μ is:
(μ)=ML−1T−2A−2
- This matches with option (iv) in List - II.
4. Magnetization (M):
- The magnetization M is defined as:
M=magnetic dipole momentvolume
- The dimensions of magnetic dipole moment are AL2 and volume is L3.
- Thus, the dimensions of magnetization are:
M=AL2L3=AL−1
- Thus, the dimensional formula for magnetization M is:
(M)=AL−1
- This matches with option (ii) in List - II.
Final Matching:
- (A) Magnetic Induction → (iii) MT−2A−1
- (B) Magnetic Flux → (i) ML2T−2A−1
- (C) Magnetic Permeability → (iv) ML−1T−2A−2
- (D) Magnetization → (ii) AL−1
Answer:
The correct matches are:
- A → iii
- B → i
- C → iv
- D → ii
- The formula for the magnetic induction B can be derived from the force on a current-carrying wire in a magnetic field:
F=I⋅L⋅B
- Rearranging gives:
B=FI⋅L
- The dimensions of force F are MLT−2, current I has dimensions A, and length L has dimensions L.
- Therefore, substituting these into the equation gives:
B=MLT−2A⋅L=MT−2A
- Thus, the dimensional formula for magnetic induction B is:
(B)=MT−2A−1
- This matches with option (iii) in List - II.
- The formula for magnetic flux Φ is given by:
Φ=B⋅S
- Where S is the area. The dimensions of area S are L2.
- Substituting the dimensions of B:
Φ=(MT−2A−1)⋅(L2)=ML2T−2A−1
- Thus, the dimensional formula for magnetic flux Φ is:
(Φ)=ML2T−2A−1
- This matches with option (i) in List - II.
- The magnetic permeability μ is defined as:
μ=BH
- We already have B and need to find H (magnetic field strength). The dimensions of H are:
H=Bμ
- The dimensions of H are AL−1.
- Substituting the dimensions of B:
μ=MT−2A−1AL−1=MT−2A2
- Thus, the dimensional formula for magnetic permeability μ is:
(μ)=ML−1T−2A−2
- This matches with option (iv) in List - II.
- The magnetization M is defined as:
M=magnetic dipole momentvolume
- The dimensions of magnetic dipole moment are AL2 and volume is L3.
- Thus, the dimensions of magnetization are:
M=AL2L3=AL−1
- Thus, the dimensional formula for magnetization M is:
(M)=AL−1
- This matches with option (ii) in List - II.
- (A) Magnetic Induction → (iii) MT−2A−1
- (B) Magnetic Flux → (i) ML2T−2A−1
- (C) Magnetic Permeability → (iv) ML−1T−2A−2
- (D) Magnetization → (ii) AL−1
The correct matches are:
- A → iii
- B → i
- C → iv
- D → ii
Similar Questions
Match List I with List II :
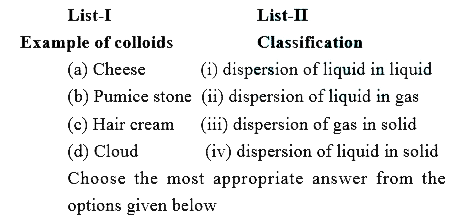
Choose the most appropriate answer from the options given below
View SolutionMatch List-I with List -II :
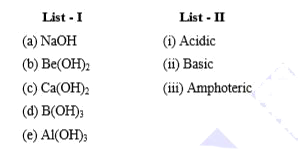 :
:
Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List - II.

Choose the most appropriate answer from the options given below :
View SolutionMatch List-I with List-II :

Choose the most appropriate answer from the options given below :
View SolutionMatch List-I with List-II :

Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List -II

Choose the most appropriate answer from the options given below :
View SolutionMatch List -I with List -II :
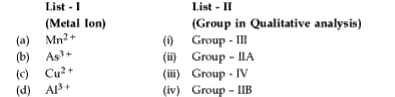
Choose the most appropriate answer from the options given below :
View SolutionMatch list - I with List - II : Choose the most appropriate answer from the options given below :
View Solution
