The sum of two forces →P and →Q is →R such that ∣∣→R∣∣=∣∣→P∣∣ .The angle θ (in degrees) that the resultant of 2→P and →Q will make with →Q is
∣∣→P+→Q∣∣=∣∣→P∣∣
P2+Q2+2PQcosθ=P2
⇒Q=2Pcosθ=0
⇒cosθ=−Q2P
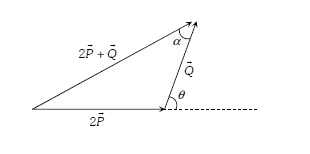
tanα=2Psinθ2Pcosθ+Q=∞[∵2Pcosθ+Q−0]
α=90∘
Similar Questions
The sum of two forces →P and →Q is →R such that ∣∣→R∣∣=∣∣→P∣∣ .The angle θ (in degrees) that the resultant of 2→P and →Q will make with →Q is
View SolutionIf vec P+ vec Q = vec R and |vec P| = |vec Q| = | vec R| , then angle between vec P and vec Q is
View SolutionThree vectors vec(P), vec(Q), vec(R) obey vec(P) + vec(Q) = vec(R) and P^(2) + Q^(2) = R^(2) the angle between vec(P) & vec(Q) is
View SolutionGiven that P=Q=R. If →P+→Q=→R then the angle between →P and →R is θ1. If →P+→Q+→R=→0 then the angle between →P and →R is θ2. The relation between θ1 and θ2 is :-
View SolutionIF →p×→q=→r and →q×→r=→p then
View SolutionProve that [vec(p) - vec(q) vec(q) - vec(r) vec(r) - vec(p)] = 0
View SolutionLet vec(p),vec(q),vec(r) be three unit vectors such that vec(p)xxvec(q)=vec(r) . If vec(a) is any vector such that [vec(a),vec(q),vec(r )]=1,[vec(a),vec(r),vec(p )]=2 , and [vec(a),vec(p),vec(q )]=3 , then vec(a)=
View SolutionColumn- IColumn II(Operation of nonzero vectors→Pand→Q)(Possivle angle between→Pand→Q)(A)∣∣→P×→Q∣∣=0(P) 90∘(B)∣∣→P×→Q∣∣=√3→P.→Q(Q) 180∘(C)→P+→Q=→RandP+Q=R(R) 60∘(D)∣∣→P+→Q∣∣=∣∣→P−→Q∣∣(S) 0∘(T) 30∘
View Solution