If ˆi,ˆj and ˆk represent unit vectors along the x, y and z axes respectively, then the angle θ between the vectors (ˆi+ˆj+ˆk) and (ˆi+ˆj) is equal to :
A
sin−1(1√3)
B
sin−1(√23)
C
cos−1(1√3)
D
90∘
Video Solution
Text Solution
The correct Answer is:A
Since →A.→B=ABcosθ
⇒cosθ=→A.→BAB=(ˆi+ˆj+ˆk)(ˆi+ˆj)√12+12+12√12+12
⇒cosθ=2√6=√23
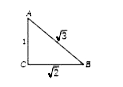
⇒sinθ=1√3
⇒θ=sin−1(1√3)
|
Similar Questions
सदिशों ˆi+ˆj+ˆk तथा ˆi−ˆj−ˆk के बीच का कोण ज्ञात कीजिये।
View Solutionसदिशों ˆi+ˆj+ˆk तथा ˆi−ˆj+ˆk के बीच का कोण ज्ञात कीजिये।
View SolutionThe unit vector perpendicular to the vectors ˆi−ˆj+ˆk,2ˆi+3ˆj−ˆk is
View SolutionFind angle θbetween the vectors →a=ˆi+ˆj−ˆkand →b=ˆi−ˆj+ˆk.
View SolutionIf hat(i), hat(j) and hat(k) are unit vectors along x,y and z-axis respectively, the angle theta between the vector hat(i) + hat(j) + hat(k)" ""and vector" hat(j) is given by
View SolutionUnit vector along the vector ˆi+ˆj+ˆk is
View SolutionIf hat(i), hat(j) and hat(k) represent unit vectors along the x, y and z axes respectively, then the angle theta between the vectors (hat(i) + hat(j) + hat(k)) and (hat(i) + hat(j)) is equal to :
View SolutionFind angle θ between the vectors →a=ˆi+ˆj−ˆk and →b=ˆi−ˆj+ˆk
View Solution