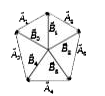
The five sides of a regular pentagon are represented by vectors ${\to A}_{1}, {\to A}_{2}, {\to A}_{3}, {\to A}_{4}$ and ${\to A}_{5}$ in cyclic order as shown. Corresponding vertices are represented by ${\to B}_{1}, {\to B}_{2}, {\to B}_{3}, {\to B}_{4} and {\to B}_{5}$ drawn from the centre of the pentagon. Then, ${\to B}_{2} + {\to B}_{3} + {\to B}_{4} + {\to B}_{5}$ =

${\to A}_{1}$

$- {\to A}_{1}$

${\to B}_{1}$

$- {\to B}_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Since, ${\to B}_{1} + {\to B}_{2} + {\to B}_{3} + {\to B}_{4} + {\to B}_{5} = 0$
This is because of regular pentagon Hence, ${\to B}_{2} + {\to B}_{3} + {\to B}_{4} + {\to B}_{5} = - {\to B}_{1}$

Updated on:21/07/2023

Class 11 PHYSICS BASIC MATHEMATICS

Similar Questions

Let $\to a$ , $\to b$ , $\to c$ are three vectors , such that $\to a$ + $\to b$ + $\to c$ = $\to 0$ .If , $| \to a | = 3$ , $∣ ∣ \to b ∣ ∣ = 4$ and
| $\to c ∣ = 5$ , then the value of, ${∣ ∣ \to a + \to b ∣ ∣}^{2}$ + ${∣ ∣ \to b - \to c ∣ ∣}^{2}$ + ${| \to c + \to a |}^{2}$ , equal to :
06:28
View Solution
Find $∣ ∣ \to a - \to b ∣ ∣,$ if two vector $\to a$ and $\to b$ are such that $| \to a | = 2, ∣ ∣ \to b ∣ ∣ = 3$ and $\to a . \to b = 4$ .
02:16
View Solution
Let $\to a and \to b$ be unit vectors such that $∣ ∣ \to a + \to b ∣ ∣ = \sqrt{3}$ . Then find the value of $(2 \to a + 5 \to b) . ((3 \to a + \to b + \to a \times \to b)) .$
04:17
View Solution
If two vectors $\to a and \to b$ are such that $| \to a | = 2, ∣ ∣ \to b ∣ ∣ = 1 and \to a . \to b = 1$ , find $(3 \to a - 5 \to b) . 2 \to a + 7 \to b .$
04:08
View Solution
Find $∣ ∣ \to a - \to b ∣ ∣$ , if two vectors $\to a$ and $\to b$ are such that $| \to a | = 2, ∣ ∣ \to b ∣ ∣ = 3$ and $\to a . \to b = 4$ .
02:04
View Solution
यदि $\to a, \to b, \to c$ अशून्य असमतलीय सदिश हो, तब ${\to r}_{1} = 2 \to a - 3 \to b + \to c, {\to r}_{2} = 3 \to a - 5 \to b + 2 \to c, {\to r}_{3} = 4 \to a - 5 \to b + \to c$
View Solution
If $\to a and \to b$ are two vectors such that $| \to a | = 2, ∣ ∣ \to b ∣ ∣ = 3 and \to a \cdot \to b = 4$ then find the value of $∣ ∣ \to a - \to b ∣ ∣$
02:45
View Solution
Let $\to a, \to b, \to c$ be three linearly independent vectors, tehn $\frac{[\to a + 2 \to b - \to c 2 \to a + \to b + \to c 4 \to a - \to b + 5 \to c]}{[a b c]} =$ 1. $0$ 2. $1$ 3. $2$ 4. $- 1$ 5. -2
02:39
View Solution

The five sides of a regular pentagon are represented by vectors →A1,→A2,→A3,→A4 and →A5 in cyclic order as shown. Corresponding vertices are represented by →B1,→B2,→B3,→B4and→B5 drawn from the centre of the pentagon. Then, →B2+→B3+→B4+→B5=

The correct Answer is:D

Since, →B1+→B2+→B3+→B4+→B5=0 This is because of regular pentagon Hence, →B2+→B3+→B4+→B5=−→B1

Similar Questions

Recommended Questions

Since, ${\to B}_{1} + {\to B}_{2} + {\to B}_{3} + {\to B}_{4} + {\to B}_{5} = 0$
This is because of regular pentagon Hence, ${\to B}_{2} + {\to B}_{3} + {\to B}_{4} + {\to B}_{5} = - {\to B}_{1}$