Direction: In the given question, read the given statement and compare the two given quantities on its basis.
Three equal circles are drawn on a triangle ABC, with points A, B, C as the centres. Radius of each of the circle is equal to half of the side of the triangle ABC (Figure not to scale)
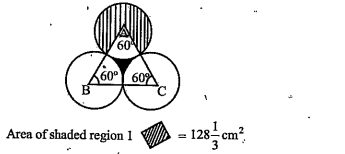
Quantity I. The area of the shaded region 2
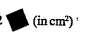
Quantity II. 30cm2
Quantity I > Quantity II
Quantity I ≤ Quantity II
Quantity I = Quantity II or No relation
Quantity I < Quantity II
The correct Answer is:D
Step by step video & text solution for Direction: In the given question, read the given statement and compare the two given quantities on its basis.Three equal circles are drawn on a triangle ABC, with points A, B, C as the centres. Radius of each of the circle is equal to half of the side of the triangle ABC (Figure not to scale)Quantity I. The area of the shaded region 2Quantity II. 30 cm^2 by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (U
View SolutionIn the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O' are centres of the circles. Find the area of shaded region
View Solution
Knowledge Check
In the given figure there are 3 semicircles , the radii of each smaller circle is equal. If the radius of the larger circle be 22 cm , then the area of the shaded region is :
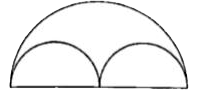 A363π4B363π3C236.5πD363π
A363π4B363π3C236.5πD363πABC is a an equilateral triangle of side 2 cm . With A , B , C as centres and radius 1 cm three arcs are drawn . The area of the region within the triangle bounded by the three arcs is
A(3√3−π2)cm2B(√3−3π2)cm2C(√3−π2)cm2D(π2−√3)cm2ABC is an equilateral triangle of side 2 cm. With A, B, C as centre and radius 1 cm three arcs are drawn. The area of the region within the triangle bounded by the three arcs is
A(a) (3√3−π2)cm2B(b) (√3−3π2)cm2C(c) (√3−π2)cm2D(d) (π2−√3)cm2
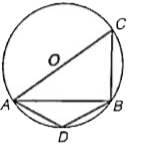
In the given diagram, 'O' is the centre of the circle and AC is the diameter. ∠ADB is 120∘. Radius of the circle is 6 cm, what is the area of the triangle ABC?
View SolutionConstruct a triangle similar to a given triangle ABC with its sides equal to 34 of the corresponding sides of the triangle ABC (i.e., of scale factor 34).
View SolutionConstruct a triangle similar to a given triangle ABC with its sides equal to 53 of the corresponding sides of the triangle ABC (i.e., of scale factor 53).
View SolutionIn the equilateral triangle ABC given below, AD = DB and AE = EC. If I is the length of a side of the triangle, then what is the area of the shaded region ?
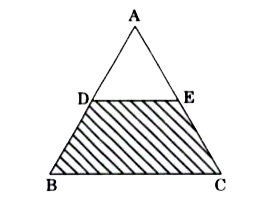
View SolutionWhat is the area of the shaded region show, if the radius of each circle is equal to the side of the hexagon, which in turn is equal to 6 cm, and A and B are the centres of the circles?
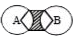
View Solution
