When does the growth rate of a population following the logistic model equal zero ? The logistic model is given as dN/dt = rN(1-N/K):
When N/K is exactly equal to one
When N nears the carrying capacity of the habitat
When N/K equals zero
When the death rate is greater than the birth rate
The correct Answer is:A
When N/K is exactly one
dNdt=rN(1−1)
dNdt=0 (Population growth is zero)
When K >N
dNdt=rN[K>>NK]
Population is expanding
When N > K
Population is declining.
Similar Questions
What is 'r' in the population equation given : dN/dt = rN
View SolutionStudy the population growth curves in the graph given below and answer the questions which follow :
(i) Identify the growth curves ‘a’ and ‘b’.
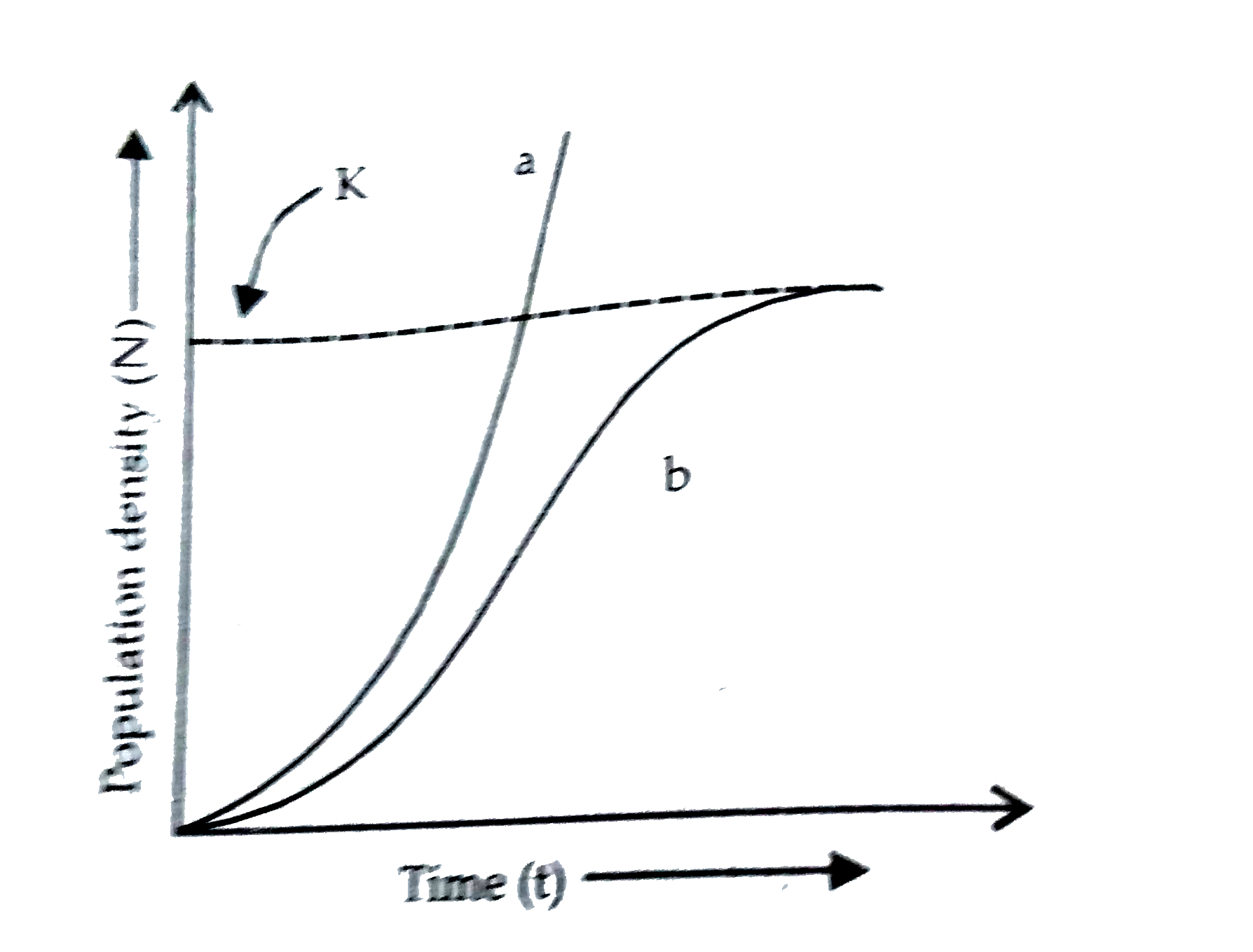
(ii) Which one. of them is considered a more realistic one and why ?
If dN9dt)=rN(K−NK) is the equation of the logistic growth curve, what does K stand for ?
(iv) What is symbolised by N ?View Solution
Knowledge Check
- Question 1 - Select One
When does the growth rate of a population following the logistic model equal zero ? The logistic model is given as dN/dt = rN(1-N/K):
Awhen N/K is exactly one.Bwhen N nears the carrying capacity of the habitat.Cwhen N/K equals zero.Dwhen death rate is greater than birth rate. - Question 2 - Select One
Which of the following is not an assumption of the logistic model for population growth?
AMembers of the population complete for resources at high densityBAll individuals have the same effect on population growthCPopulation growth rate increases as the size of the population approaches the carrying capacityDThere is no time lag between birth and the time an organism begins to affect population growth - Question 3 - Select One
Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The population growth is generally descibed by the following equations :
dN/dt=rN(K−N)/K
What does 'r' represent in the given equation ?APopulation density at time Y.BIntrinsic rate of natural increaseCCarrying capacityDThe base of natural logarithum
According to the logistic population growth model, the growth rate is independent of
View SolutionPopulation Growth|Growth Models|Exponential Growth|Logistic Growth|NCERT
View Solutionwhich of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacityView SolutionRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The equations correctly represents Verhulst-Pearl logistic growth is:View SolutionRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Identify the incorrect statement :View Solution
