H-परमाणु के Is-कक्षक के लिए रेडियल तरंग फलन निम्नवत् है।,
(जहाँ )
पर इलेक्ट्रॉन पाये जाने की रेडियल प्रायिकता घनत्व (radial probability density) तथा नाभिक पर इलेक्ट्रॉन पाये जाने की रेडियल प्रायिकता घनत्व है। (x + y) का मान ज्ञात करो।
The correct Answer is:3
1s कक्षक के लिए
Similar Questions
The wave function of 2s electron is given by
W2s=14√2π(1a0)3/2(2−ra0)e−1a0
It has a node at r=rp .Find the radiation between rp and a
View Solution298 K पर N2 गैस की जल में विलेयता के लिए हेनरी नियम का स्थिरांक 1×10−5 atm है। वायु में N2 का मोल प्रभाज 0.8 है। यदि 298 K और 5 atm पर जल के 10 मोल में विलेय वायु के N2 के मोलों की संख्या x⋅10−4 है, तो x का मान ज्ञात कीजिए।
View Solution
Knowledge Check
H के प्रथम कक्षक को निम्न द्वारा निरूपित किया जाता है: ψ=1√r(1a0)3/2e−r/a0,
जहाँ, a0 बोर त्रिज्या है। क्षेत्र dV में नाभिक से r दूरी पर स्थित इलेक्ट्रॉन के पाए जाने की प्रायिकता क्या होगी?Aψ2drB∫ψ24πr2dVCψ24πr2drD∫ψdVनाभिक से r दूरी पर, अनंत मोटाई dr, के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4πr2dr है | पर P की निर्भरता का गुणात्मक चित्र है :
A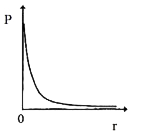 B
B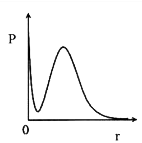 C
C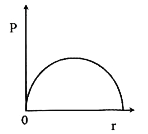 D
D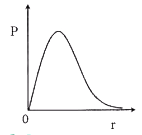
नाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
A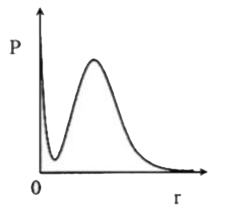 B
B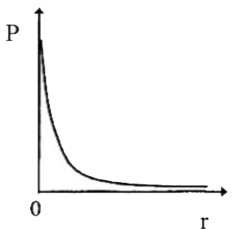 C
C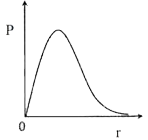 D
D
हाइड्रोजन परमाणु के लिए त्रिज्य तरंग समीकरण ϕ=116√41(aσ)32[(x−1)(x2−8x+12)]e−12 है।
जहां x=2xa0,a0 प्रथम बोर कक्षा की त्रिज्या। नाभिक से त्रिज्य नोड की न्यूनतम और अधिकतम दूरी (स्थिति) है:
View SolutionThe first obrital of H or H like atom is represencted by
ψ=1√π(Za0)3/2e−ze/a0
where a0= Bohr's orbit . The actual probability of fiding the elercrton at a distance r form the nucleus is :
View Solutionएक परमाणु में, दो इलेक्ट्रॉन नाभिक के चारों त्रिज्या r और 4r की वृत्ताकार कक्षाओं में परिक्रमण करते हैं। एक परिक्रमण को पूर्ण करने के लिए उनके द्वारा लिए गए समय का अनुपात (T2:T1) है:
View SolutionThe Schrodinger wave equation for hydrogen atom is ψ2s=14√2π(1a0)3/2(2−ra0)e−t/a0
where a0 is Bohr's radius. If the radial node in 2 s be at r0, then r0 would be equal to
View Solutionयदि 1 atm दाब और 500 K पर 18 gm/mole मोलर द्रव्यमान के पदार्थ का वाष्प घनत्व 0.36kgm−3 है, तो वाष्प के लिए Z का मान है: (R=0.082L atm mole−1K−1 लीजिए)
View Solution
