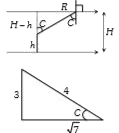
On a bright sunny day a diver of height h stands at the bottom of a lake of depth H. Looking upward, he can see objects outside the lake in a circular region of radius R. Beyond this circle he sees the image of objects lying on the floor of the lake. If refractive index of water is 4/3, then the value of R is–
3(H−h)√7
3h √7
H−h√73
(H−h)√53
The correct Answer is:A
n2sinC=n1sin90
43sinC=1⇒sinC−34
tanC=3√7=RH−h
R=3√7(H−h).
Topper's Solved these Questions
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( Refraction at Curved surface )
61 Videos
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( Prism Theory & Dispersion of Light )
46 Videos
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS (Refraction of Light at Plane Surfaces)
48 Videos
- MAGNETISMBOOK - ERRORLESSCHAPTER - MAGNETISMEXERCISE - Assertion and Reason
22 Videos
- WAVE OPTICS AND ELECTROMAGNETIC THEORYBOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - ASSERTION & REASON
27 Videos
Similar Questions
A luminous object O is located at the bottom of a big pool of liquid of refractive index μ and depth h. The object O emits rays upwards in all directions, so that a circle of light is formed at the surface of the liquid by the rays which are refracted into the air. what happens to the rays beyond the circle ? Determine the radius and the area of the circle .
View SolutionA fish looking up through the water sees the outside world contained in circular horizon. If the R.I. of water 43 and tne fish is 12 cm below the surface, the radius of this circle in cm is-
View Solution
Knowledge Check
A diver looking up through the water sees the outside world contained in a circular horizon. The refractive index of water is 43, and the diver's eyes are 15 cm below the surface of 3 water. Then the radius of the circle is:
A15×3×√5cmB15×3√7cmC15×√73cmD15×3√7cmA fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 43 and the fish is 12 cm below the surface, the radius of this circle is cm is
A36√7B36√7C4√5D36√5A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 4/3 and the fish is 12cm below the surface, the radius of this circle in cm is
A36√5B4√5C36√7D36/√7
If we see the outside objects by keeping an eye at a depth h inside water, then the value of RADIUS of circle of view for outside objects will be
View SolutionA fish looking up through the wave sees the outside world contained in a circular horizon. If the refractive index of water is 43 and the fish is 12 cm below the surface, the radius of this circle in cm is
View SolutionA fish situated at a depth h below the surface of water in a lake ,can see the outside objects in air through a circular aperature of radius r . What is the radius of the aperture in terms of h and n ,where n=anw? [anw = R.I. of water w.r.t. air]
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
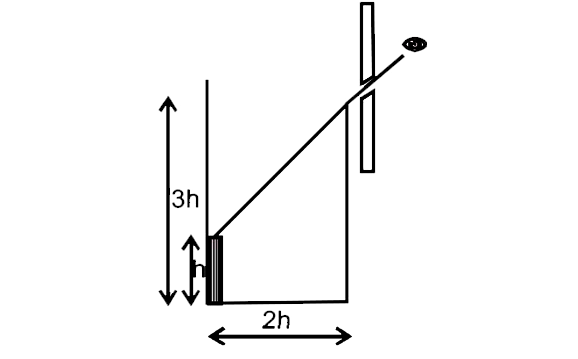
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View Solution
