One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
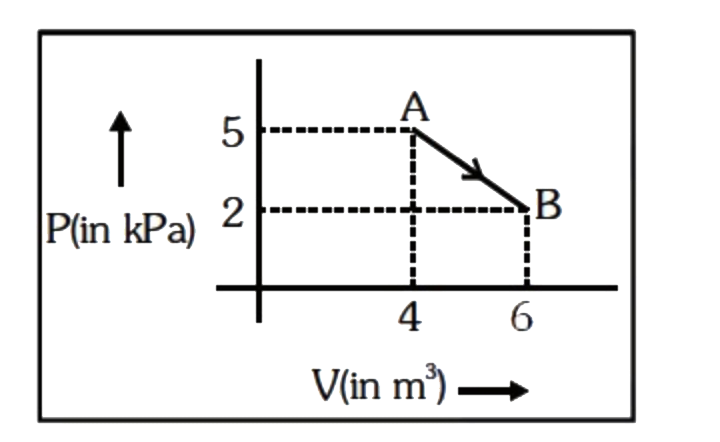
The change in internal energy of the gas during the transition is :
−20kJ
20J
−12kJ
20kJ
The correct Answer is:A
ΔU=f2nRΔT f→ degree of freedom
⇒ΔU=52(PfVf−PiVi)
=52(2×103×6−5×103×4)=−20kJ.
Topper's Solved these Questions
- KINETIC THEORY OF GASES Book:ERRORLESSChapter:KINETIC THEORY OF GASES Exercise:ASSERTION AND REASON
Explore 16 Videos
- KINETIC THEORY OF GASES Book:ERRORLESSChapter:KINETIC THEORY OF GASES Exercise:NCERT BASED QUESTIONS (Pressure and Energy)
Explore 31 Videos
- GRAVITATIONBook:ERRORLESSChapter:GRAVITATIONExercise:Assertion and Reason
Explore 25 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESSChapter:MOTION IN ONE DIMENSIONExercise:ASSERTION AND REASON
Explore 24 Videos
Similar Questions
Knowledge Check
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
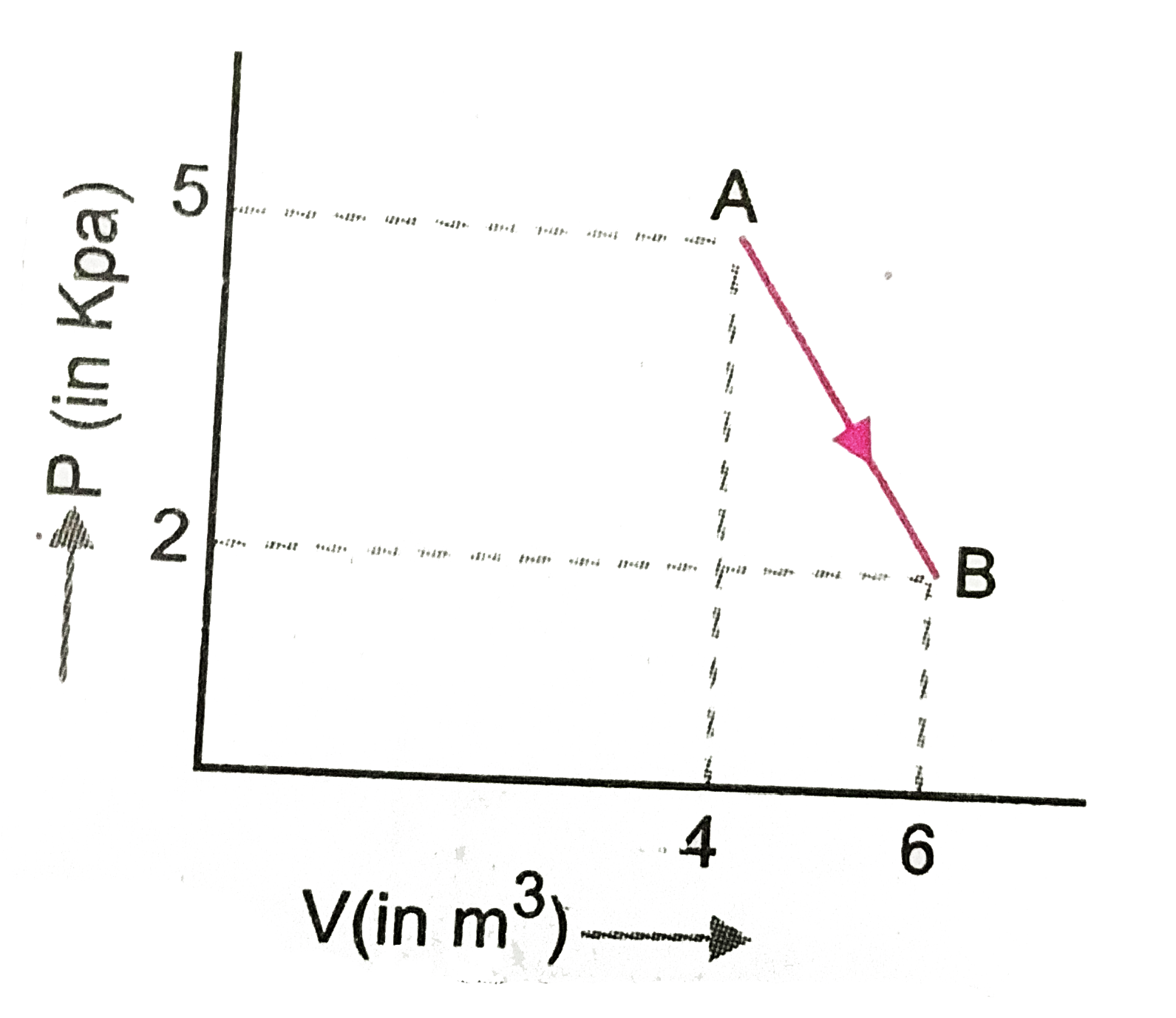 A−20KJB20KJC−12KJD20KJ
A−20KJB20KJC−12KJD20KJOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
 A−20KJB20 JC−12KJD20 KJ
A−20KJB20 JC−12KJD20 KJA mono-atomic gas is taken along path AB as shown. Calculate change in internal energy of the gas.
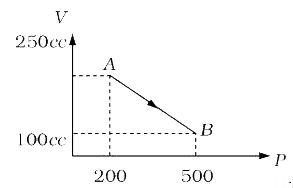 A279.8JB341JC241JDzero
A279.8JB341JC241JDzero
One mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure. Then the change in the energy in expanding the gas from a to c along the path abc is:

View SolutionOne mole of an ideal mono-atomic gas is caused to go through the cycle shown in the figure below. Then the change in the internal enegry in expanding the gas from a to c along the path abc is:
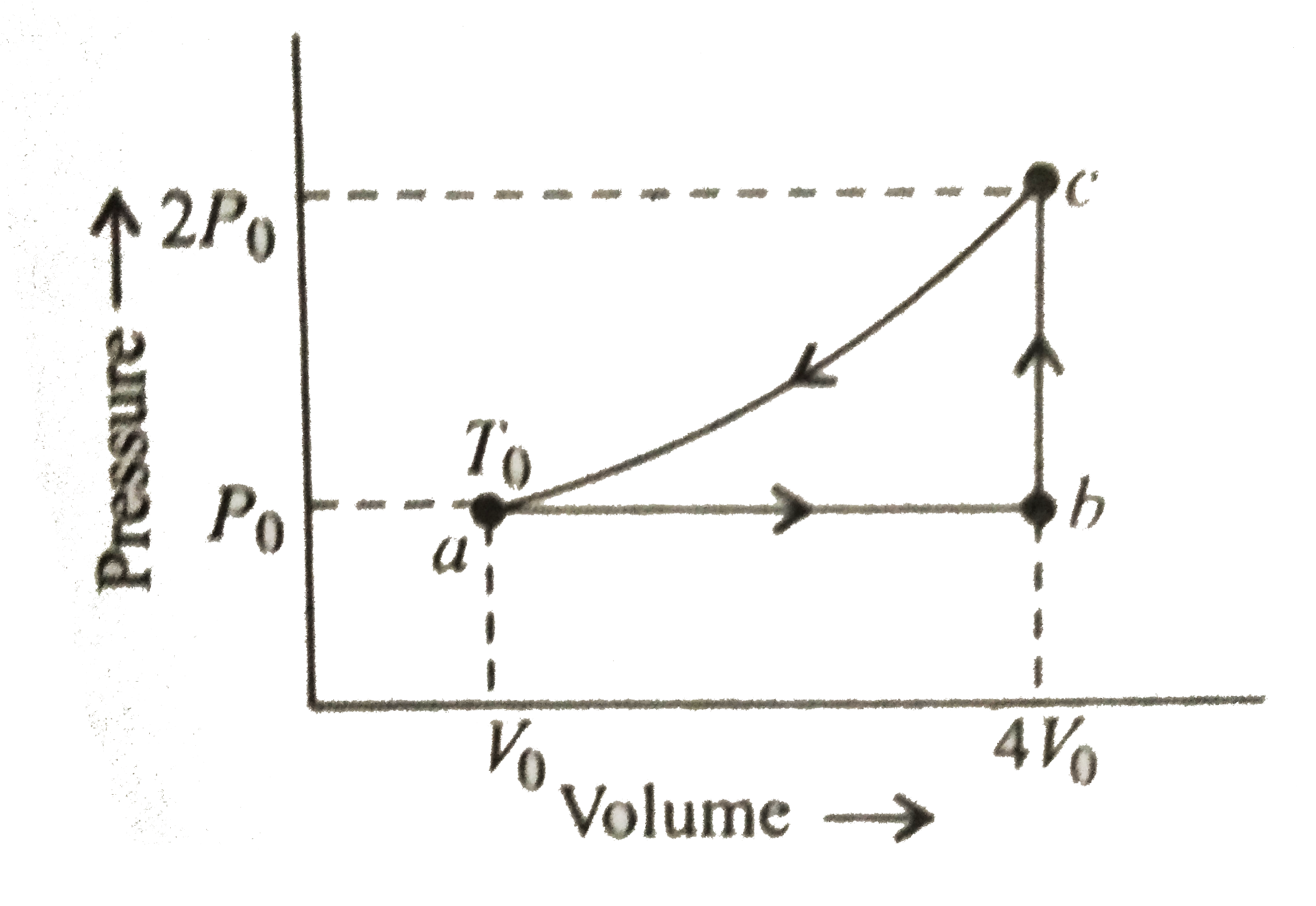
View SolutionAn ideal gas is taken along the path AB as shown in the figure. The work done by the gas is
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
View SolutionOne mole of an ideal monoatomic gas is caused to go through the cycle shown in figure.Then the change in the internal energy of gas from a to b and b to c is respectively :

View Solution
