Volume-temperature graph at atmospheric pressure for a monoatomic gas (V in m3,T in ∘C) is

The correct Answer is:A
To determine the volume-temperature graph for a monoatomic gas at atmospheric pressure, we can use the ideal gas law and analyze the relationship between volume and temperature. Here’s a step-by-step solution:
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = temperature in Kelvin
Step 2: Rearranging the Ideal Gas Law
We can rearrange the ideal gas law to express volume V in terms of temperature T:
V=nRTP
Step 3: Convert Temperature to Kelvin
Since the temperature T is given in degrees Celsius, we need to convert it to Kelvin:
T(K)=T(°C)+273
Step 4: Substitute Temperature into the Volume Equation
Substituting the expression for T into the volume equation gives:
V=nR(T+273)P
Step 5: Identify the Linear Relationship
This equation can be rewritten as:
V=nRPT+nR⋅273P
This is in the form of a linear equation y=mx+c, where:
- y is V
- x is T
- m (the slope) is nRP
- c (the y-intercept) is nR⋅273P
Step 6: Analyze the Graph
From the linear equation, we can conclude:
- The slope m is positive, indicating that as temperature increases, volume also increases.
- The y-intercept c is also positive, which means that when T=0 (in Celsius), the volume is still positive.
Conclusion
The volume-temperature graph for a monoatomic gas at atmospheric pressure will be a straight line with a positive slope, starting from a positive y-intercept.
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = temperature in Kelvin
We can rearrange the ideal gas law to express volume V in terms of temperature T:
V=nRTP
Since the temperature T is given in degrees Celsius, we need to convert it to Kelvin:
T(K)=T(°C)+273
Substituting the expression for T into the volume equation gives:
V=nR(T+273)P
This equation can be rewritten as:
V=nRPT+nR⋅273P
This is in the form of a linear equation y=mx+c, where:
- y is V
- x is T
- m (the slope) is nRP
- c (the y-intercept) is nR⋅273P
From the linear equation, we can conclude:
- The slope m is positive, indicating that as temperature increases, volume also increases.
- The y-intercept c is also positive, which means that when T=0 (in Celsius), the volume is still positive.
The volume-temperature graph for a monoatomic gas at atmospheric pressure will be a straight line with a positive slope, starting from a positive y-intercept.
Topper's Solved these Questions
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - NCERT BASED QUESTIONS (Speed of Gas)
24 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - NCERT BASED QUESTIONS (Degree of Freedom and Specific Heat)
30 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - Assertion and Reason
25 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - ASSERTION AND REASON
24 Videos
Similar Questions
Volume occupied by an ideal gas at one atmospheric pressure and 0∘C is V ml. Its volume at 273 K will be
View SolutionSome ideal monoatomic gas A in an enclosure has a pressure P and the temperature T . Another ideal monoatomic gas B enclosed in a container of the same volume has a pressure of 2P and temperature T2. The ratio of the average kinetic energy per molecule of gas A to gas B is
View Solution
Knowledge Check
Volume-temperature graph at atmospheric pressure for a monoatomic gas (V in m3,T in ∘C) is
A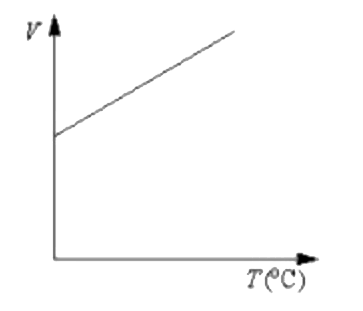 B
B C
C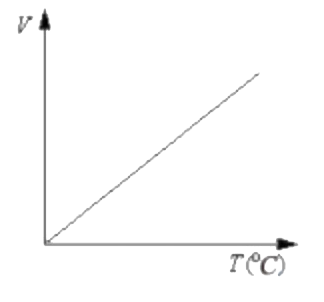 D
D
Graph for specific heat at constant volume for a monoatomic gas
A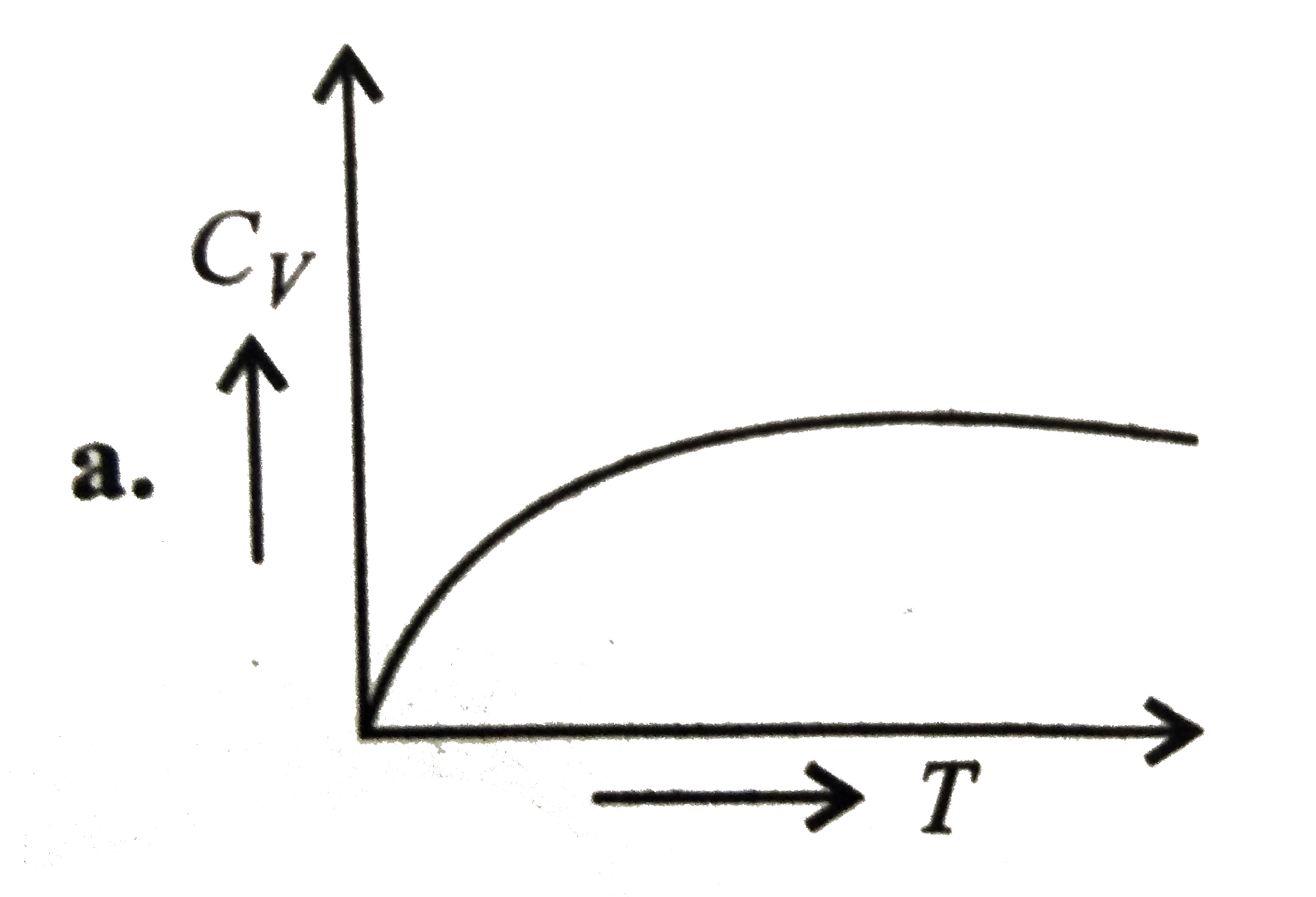 B
B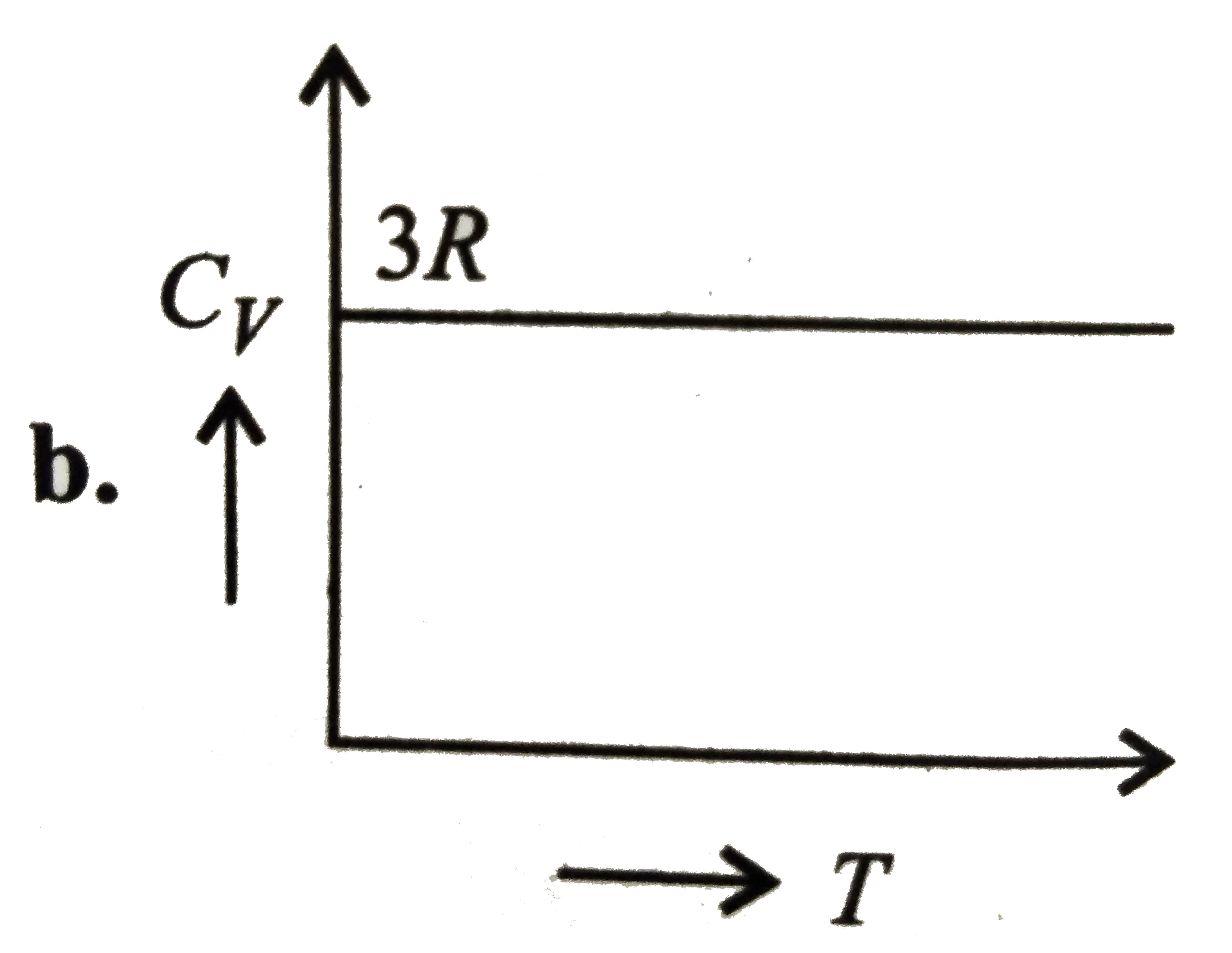 C
C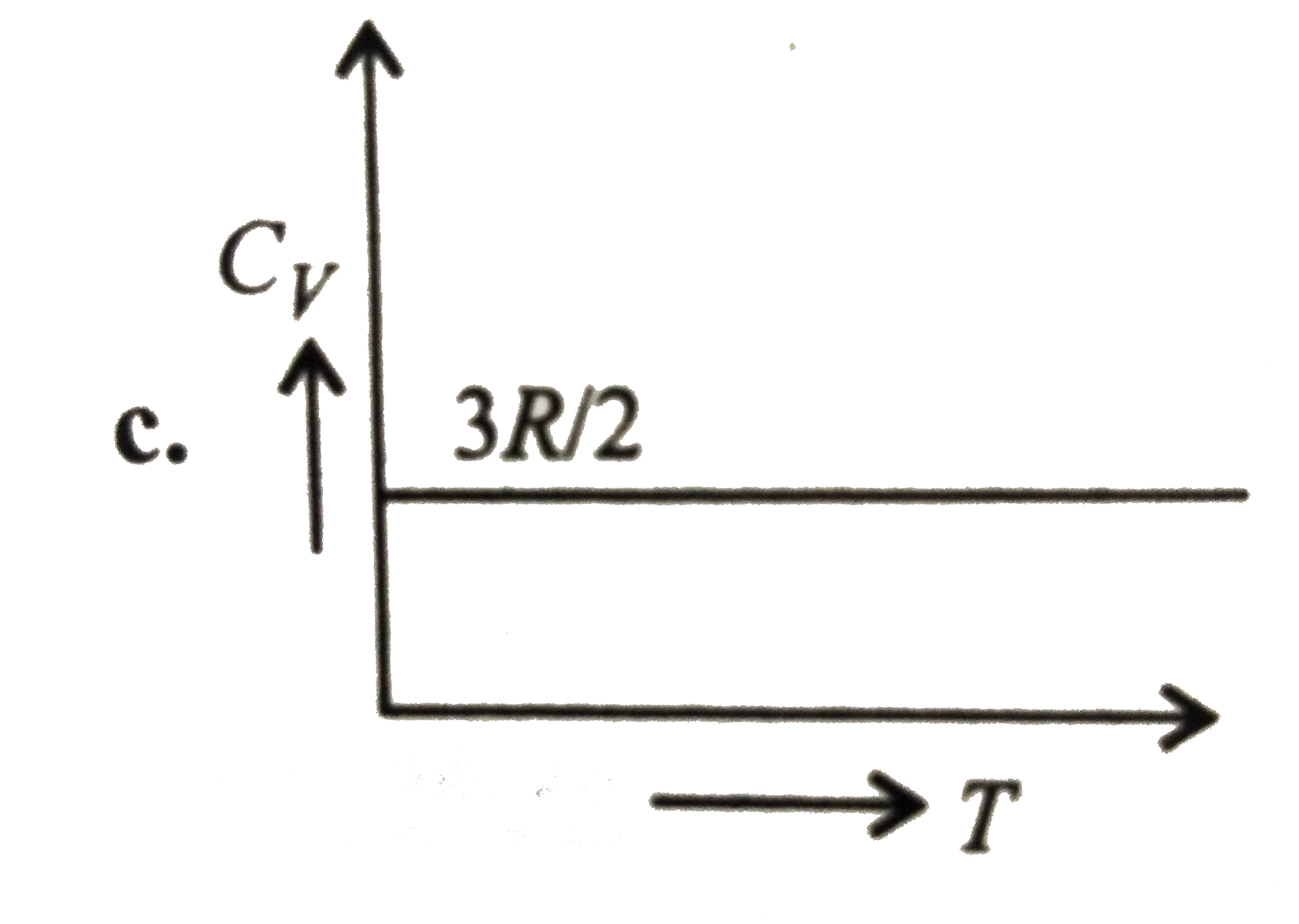 D
DGraph for specific heat at constant volume for a monoatomic gas
A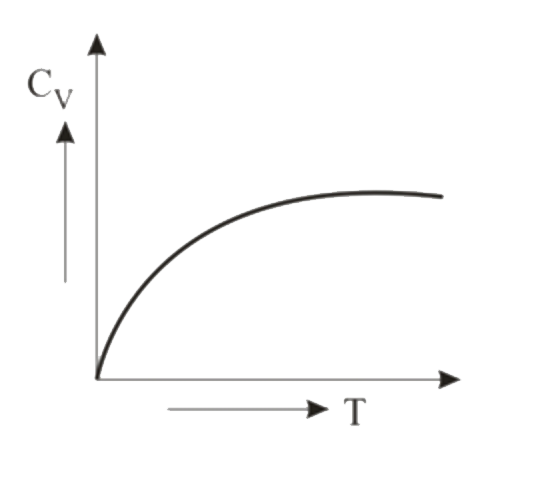 B
B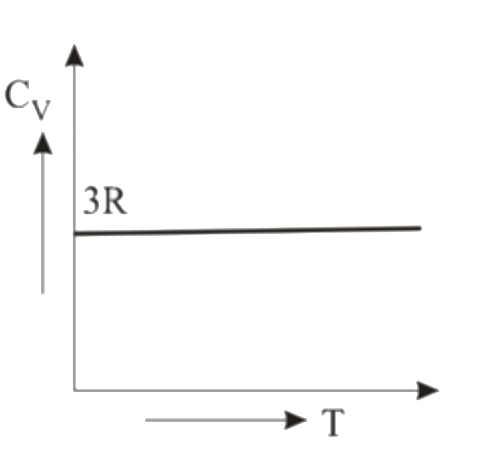 C
C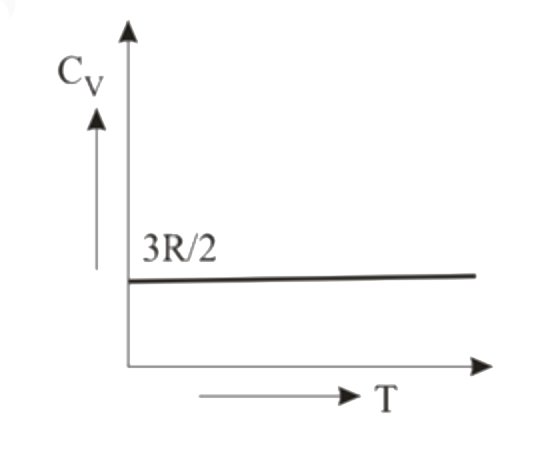 D
D
Volume occupied by an ideal gas at one atmospheric pressure and 0∘C is V ml. Its volume at 273 K will be
View SolutionVolume occupied by an ideal gas at one atmospheric pressure and 0∘C is V ml. Its volume at 273 K will be
View SolutionIf a given mass of a gas occupies a volume 100 at one atmospheric pressure and a temperature of 1000C. What will be its volume at 4 atmospheric pressure, the temperature being the same?
View SolutionIn an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
View SolutionThe temperature of a gas at pressure P and volume V is 27∘C. Keeping its volume constant. If its temperature is raised to 927∘C, then its pressure will be
View Solution
