Two stars of mass and are parts of a binary system. The radii of their orbits are and respectively, measured from the C.M. of the system. The magnitude of gravitational force exerts on is
The correct Answer is:A
To find the magnitude of the gravitational force F that mass m1 exerts on mass m2 in a binary star system, we can use Newton's law of universal gravitation. The formula for the gravitational force between two masses is given by:
F=G⋅m1⋅m2d2
where:
- F is the gravitational force,
- G is the gravitational constant (6.674×10−11N m2/kg2),
- m1 and m2 are the masses of the two stars,
- d is the distance between the two masses.
1. Identify the Distance Between the Masses:
The distance d between the two stars can be expressed in terms of their respective orbital radii r1 and r2. Since r1 and r2 are measured from the center of mass (C.M.) of the system, the total distance d between the two stars is:
d=r1+r2
2. Substitute the Distance into the Gravitational Force Formula:
Now, we can substitute d into the gravitational force formula:
F=G⋅m1⋅m2(r1+r2)2
3. Final Expression:
Thus, the magnitude of the gravitational force that mass m1 exerts on mass m2 is:
F=G⋅m1⋅m2(r1+r2)2
- F is the gravitational force,
- G is the gravitational constant (6.674×10−11N m2/kg2),
- m1 and m2 are the masses of the two stars,
- d is the distance between the two masses.
The distance d between the two stars can be expressed in terms of their respective orbital radii r1 and r2. Since r1 and r2 are measured from the center of mass (C.M.) of the system, the total distance d between the two stars is:
d=r1+r2
Now, we can substitute d into the gravitational force formula:
F=G⋅m1⋅m2(r1+r2)2
Thus, the magnitude of the gravitational force that mass m1 exerts on mass m2 is:
F=G⋅m1⋅m2(r1+r2)2
Topper's Solved these Questions
- GRAVITATIONBook:ERRORLESSChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS (Acceleration Due to Gravity)
Explore 39 Videos
- GRAVITATIONBook:ERRORLESSChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS (Gravitation Potential, Energy and Escape Velocity)
Explore 38 Videos
- FRICTION Book:ERRORLESSChapter:FRICTION Exercise:ASSERTION & REASON
Explore 8 Videos
- KINETIC THEORY OF GASES Book:ERRORLESSChapter:KINETIC THEORY OF GASES Exercise:ASSERTION AND REASON
Explore 16 Videos
Similar Questions
Knowledge Check
Two stars of mass m1 and m2 are parts of a binary star system. The radii of their orbits are r1 and r2 respectivey, measured from the centre of mass of the system. The magnitude of gravitational force m1 exerts on m2 is
Am1m2G(r1+r2)2Bm1G(r1+r2)2Cm2G(r1+r2)2DG(m1+m2)(r1+r2)2Two particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
AzeroB7Gm4r2C9Gm4r2D3Gm2r2Two bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
Am2Rm1+m2Bm1Rm1+m2Cm1m2m1+m2RDm1+m2m1R
Two cars of masses m1 and m2 are moving in circles of radiir1 and r2, respectively. Their speeds are such that they make complete circles in the same time t. The ratio of their centripetal acceleration is
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
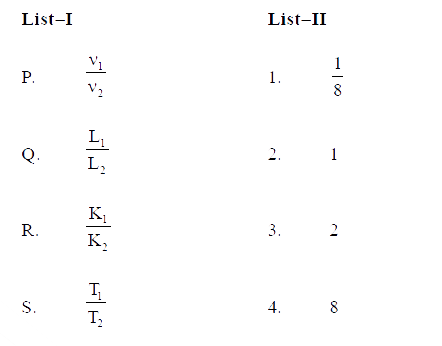
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo satellites of masses 3 m and m orbit the earth in circular orbits of radii r and 3 r respectively. The ratio of the their speeds is
View Solution

