The plot of the number (N) of decayed atoms versus activity (R) of a radioactive substance is
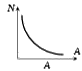
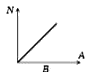

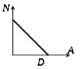
The correct Answer is:D
Ndecayed=N0−N=N0−Aλ
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Past Years Questions
67 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - NCERT BASED QUESTIONS (Nucleus, Nuclear Reaction)
57 Videos
- ALTERNATING CURRENTBOOK - ERRORLESSCHAPTER - ALTERNATING CURRENTEXERCISE - Assertion & Reason
13 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSERTION AND REASON
26 Videos
Similar Questions
Knowledge Check
99% quantity of a radioactive substance decays between
A8 and 9 half livesB7 and 8 half livesC9 and 10 half livesD6 and 7 half livesThe graph between number of decayed atoms N' of a radioactive element and time t is.
A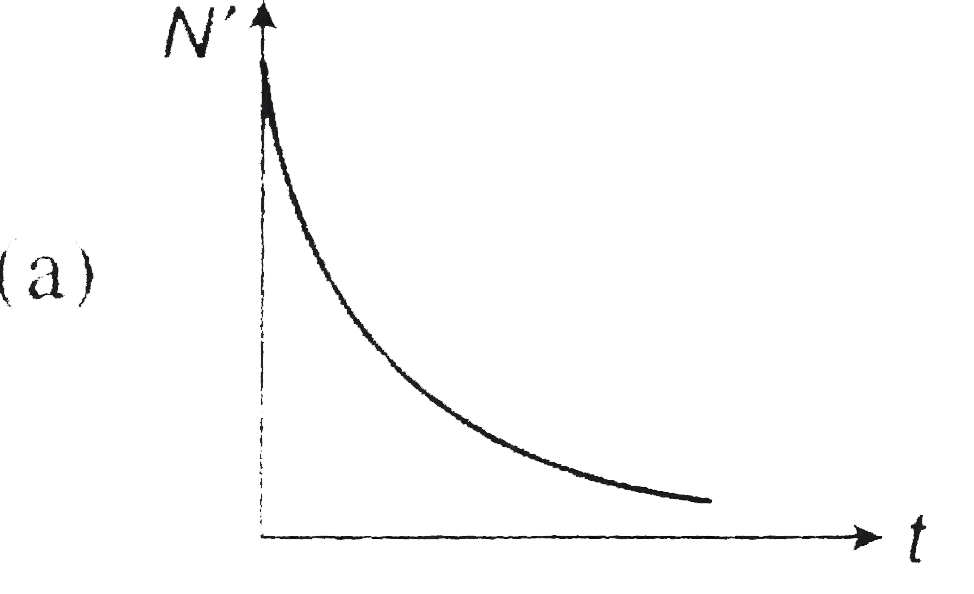 .B
.B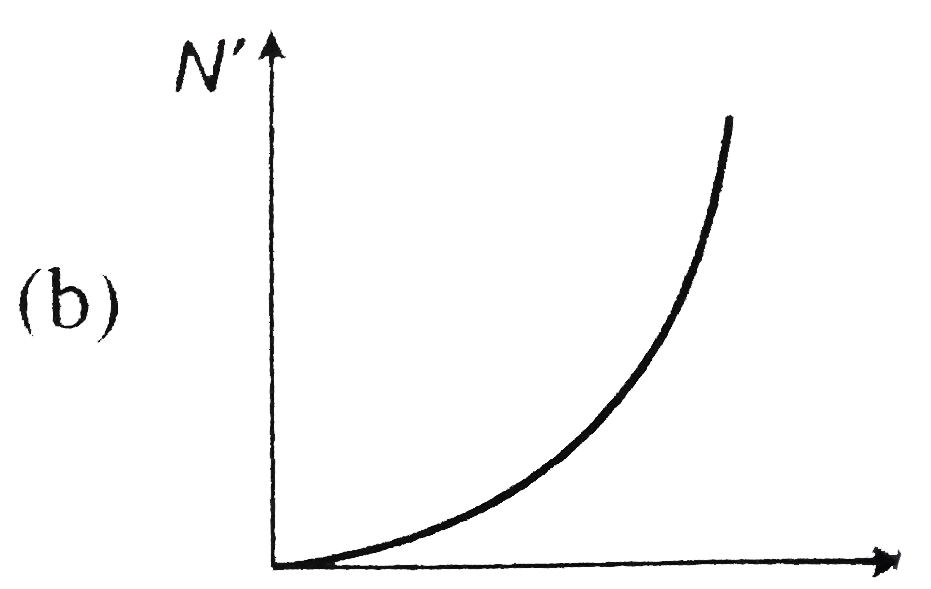 .C
.C .D
.D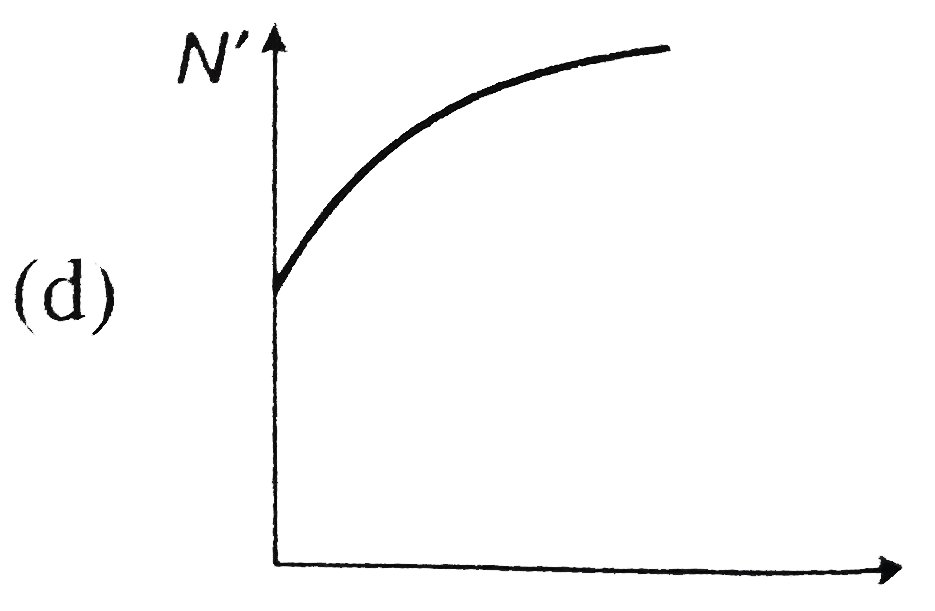 .
.The relationship between decay constant λ and half-life T of a radioactive substance is
Aλ=log102TBλ=loge2TCλ=log210TDλ=log2eT
State the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half life T1/2
Depict in the plot the number of undecayed nuclei at
(i) t=3T1/2 and (ii) t=5T1/2.
View SolutionState the law of radioactive decay.
Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half-life T12.
Depict in the plot the number of undecayed nuclei at (i) t=T12 and (ii) t=5T12.
View SolutionHalf-life of a radioactive substance is T. At time t_1 activity of a radioactive substance is R1 and at time t2 it is R2. Find the number of nuclei decayed in this interval of time.
View SolutionState the laws of radioactive decay. Define the term 'decay constant' for a radioactive substance.
View SolutionThe half-life of a radioactive substance is 30 minutes, The time (in minutes) taken between 40% decay and 85% decay of the same radioactive substance is.
View Solution
