Consider the two idealised systems (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L>>R radius of cross-section In (i) E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant the solenoid and zero outside. these idealised assumptions, however, contradict fundamental laws as below
Case (i) contradicts Gauss law for electrostatic fields
Case (ii) contradicts Gauss law for magnetic fields
Case (i) agrees with ∮ E.dl = 0
Case (ii) contradicts ∮ H.dl = Ien
The correct Answer is:B
As Gauss law states ∮sE ds = qε0 for electrostatic field . It does not contradict for electrostatic fields as the electric field lines do not form continuous closed path. According to Gauss law in magnetic field,
∮s=E.ds=0
It contradicts for magnetic field, because there is a magnetic field inside the solenoid and no field outside the solenoid carrying current but the magnetic field lines from the closed path.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT Book:ERRORLESSChapter:MAGNETIC EFFECTS OF CURRENT Exercise:NCERT BASED QUESTIONS (Motion of Charged Particle in Magnetic Field)
Explore 69 Videos
- MAGNETIC EFFECTS OF CURRENT Book:ERRORLESSChapter:MAGNETIC EFFECTS OF CURRENT Exercise:NCERT BASED QUESTIONS (Force and Torque on a Current Carrying Conductor )
Explore 51 Videos
- ELECTROSTATICSBook:ERRORLESSChapter:ELECTROSTATICSExercise:ASSERTION & REASON
Explore 25 Videos
- MAGNETISMBook:ERRORLESSChapter:MAGNETISMExercise:Assertion and Reason
Explore 22 Videos
Similar Questions
A parallel plate capacitor with plate area A and plate separation d, is charged by a constant current I. Consider a plane surface of area A/2 parallel to the plates and situated symmetrically between the plates. Determine the displacement current through this area.
View SolutionA parallel- plate capacitor with plate area A and separation between the plates d, is charged by a constant current i. Consider a plane surface of area A/2 parallel to the plates and drawn summetrically between the plates. Find the displacement current through this area.
View Solution
Knowledge Check
Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L>>R, radius of cross-section. In (i) →E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealised assumptions, however, contradict fundamental law as below:
Acase (i) contradicts Gauss's law for electrostatic fieldsBcase (ii) contradicts Gauss's law for magnetic fields.Ccase (i) agrees with ∮→E.d→l=0Dcase (i) contradicts ∮→H.d→l=lmA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
A(a) Q=ε0AVdB(b) Q=ε0KAVdC(c) E=VKdD(d) W=ε0AV22d[1−1K]
A parallel plate capacitor with plate area A and separation between the plates d, is charged by a constant current i. Consider a plane surface of area A/4 parallel to the plates and drawn symmetrically between the plates. Find the displacement current through this area.
View SolutionConsider a parallel plate capacitor is charged by a constant current I, with plate area A and separation between the plates d. Consider a plane surface of area A/4 parallel to the plates and drawn symmetrically between the plates. Find the displacement current through this area.
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionA long straight solid metal wire of radius R carries a current I, uniformly distributed over its circular cross-section. Find the magnetic field at a distance r from axis of wire (i) inside and (ii) outside the wire.
View SolutionA parallel-plate capacitor of plate area A and plate separation d is charged by a ideal battery of e.m.f. V and then the battery is disconnected. A slab of dielectric constant 2k is then inserted between the plates of the capacitor so as to fill the whole space between the plates. Find the change in potential energy of the system in the process of inserting the slab.
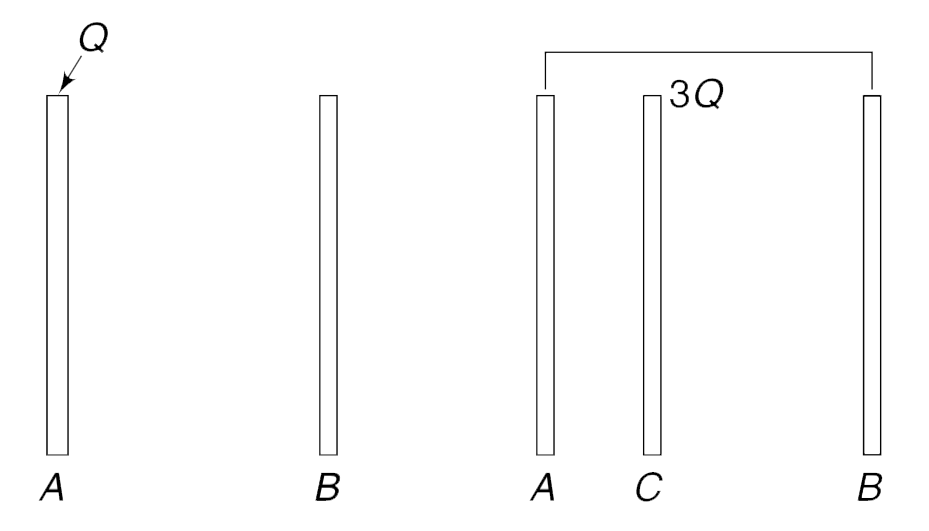
View SolutionA and B are two large identical thin metal plates placed parallel to each other at a small separation. Plate A is given a charge Q. (i) Find the amount of charge on each of the two faces of A and B. (ii) Another identical plate C having charge 3Q is inserted between plate A and B such that distance of C from B is twice its distance from A. Plate A and B is shorted using a conducting wire. Find charge on all six faces of plates A, B and C. (iii) In the situation described in (ii) the plate A is grounded. Now write the charge on all six faces.
View Solution
