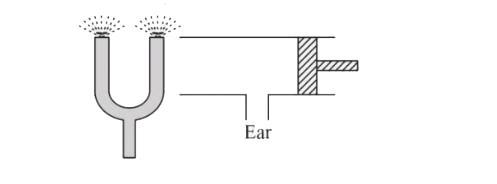
Vibrating tuning fork of frequency n is placed near the open end of a long cylindrical tube. The tube has a side opening and is fitted with a movable reflecting piston. As the piston is moved through 8.75cm, the intensity of sound changes from a maximum to minimum. If the speed of sound is 350m/s. Then n is

500 Hz
1000 Hz
2000 Hz
4000 Hz
The correct Answer is:B
When the piston is moved.
Path difference = 2×8.75=17.5cm
As intensity changes from maximum to minimum
∴ Additional path λ2=17.5⇒λ=35cm
Hence, v=fλ⇒f=vλ=3500.35=1000Hz.
Topper's Solved these Questions
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - NCERT BASED QUESTIONS (BEATS)
18 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - NCERT BASED QUESTIONS (STATIONARY WAVES)
10 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - NCERT BASED QUESTIONS (PROGRESSIVE WAVES)
24 Videos
- UNITS, DIMENSIONS AND MEASUREMENTBOOK - ERRORLESSCHAPTER - UNITS, DIMENSIONS AND MEASUREMENTEXERCISE - ASSERTION & REASON
17 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - ASSERTION & REASON
22 Videos
Similar Questions
A vibrating tuning fork of frequency n is placed near the open end of a long cylindrical tube. The tube has a side opening and is also fitted with a movable reflecting piston. As the piston is moved through 8.75 cm, the intensity of sound just changes from a maximum to minimum. If the speed of sound is
350 metre per second, the value of n is N3 then N is.
View SolutionIn Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340ms−1.
View Solution
Knowledge Check
Vibrating tuning fork of frequency v is placed near the open end of a long cylindrical tube. The tube has a side opening and is fitted with a movable reflecting piston. As the piston is moved through 8.75 cm, the intensity of sound changes from a maximum to minimum, if the speed of sound is 350 m/s. Then v is
 A500 HzB1000 HzC2000 HzD4000 Hz
A500 HzB1000 HzC2000 HzD4000 HzA long cylindrical tube carries a highly polished piston and has a side opening . A tuning fork of frequency n is sounded at the open end of the tube . The intensity of the sounded heard by the listener changes if the piston is moved in or out. At a particular position of the piston he hears a maximum sound . When the piston is moved through a distance of 9cm, the intensity of sound becomes minimum. If the speed of sound is 360m/s, the value of n is
 A129.6HzB500HzC1000HzD2000Hz
A129.6HzB500HzC1000HzD2000HzA tuning fork of frequency n is held near the open end of tube, the tube is adjusted until resonance occurs. If the two shortest lengths to produce resonance are L1andL2 , then the speed of the sound is
An(L2−L1)Bn(L2−L1)2C4n(L2−L1)D2n(L2−L1)
A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water , figure. The water level in the tube is gradually lowerd. When the water level is 17cm below the open end, maximum intensity of sound in heard. If the room temperature is 20∘C, calculate
(a) speed of sound in air at room temperature.
(b) speed of sound in air at 0∘C
(c) if the water in the tube is replaced with mercury, will there be any difference in your observations?

View SolutionA tunning fork of frequency 340Hz is vibrated just above a cylindrical tube. The length of the tube is L=120cm. Water is slowly poured into the tube. Determine the minimum height of water required for resonance. ( Take velocity of sound in air v=340m/s)
View SolutionA tuning fork vibrating with a frequency of 500 Hz is kept close to the open end of a tube filled with water, as shown in figure. The water level in the tube is gradually lowered When the water level is 17 cm below the open the open end, maximum intensity of sound is heard. If the room temperature is 20∘ C, the speed of sound in air at the temperature is

View SolutionA piston fitted in cylindrical pipe is pulled as shown in the figure . A tuning fork is sounded at open end and loudest sound is heard at open length 13 cm, 41 cm and 69 cm, the frequency of tuning fork if velocity of sound is 350m/s is :
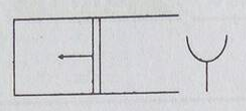
View SolutionA piston fitted in cylindrical pipe is pulled as shown in the figure . A tuning fork is sounded at open end and loudest sound is heard at open length 13 cm, 41 cm and 69 cm, the frequency of tuning fork if velocity of sound is 350m/s is :

View Solution
