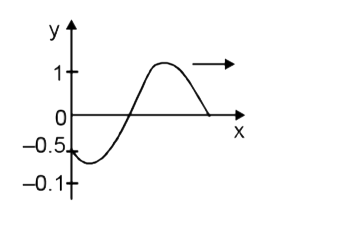
A progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:
y=−asin(kx−ωt)
y=−acos(kx+ωt)
y=asin(kx−ωt)
y=acos(kx−ωt)
The correct Answer is:B
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - NCERT BASED QUESTIONS (INTERFERENCE AND SUPERPOSITION OF WAVES)23videos
WAVES AND SOUND
- BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - NCERT BASED QUESTIONS (BEATS)18videos
WAVES AND SOUND
- BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON25videos
WAVES AND SOUND
- BOOK - ERRORLESSCHAPTER - UNITS, DIMENSIONS AND MEASUREMENTEXERCISE - ASSERTION & REASON17videos
UNITS, DIMENSIONS AND MEASUREMENT
- BOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - ASSERTION & REASON22videos
WORK, ENERGY POWER AND COLLISION
Similar Questions
Knowledge Check
- Question 1 - Select One
y(xt)=asin(kx−ωt+ϕ) represents a
Awave travelling in the negative direction of x-axisBWave travelling in the positive direction of x-axisCstationary waveDcombination of two stationary waves - Question 2 - Select One
Consider the snapshot of a wave traveling in positive x–direction
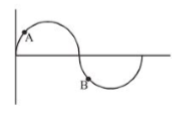AThe particle A is moving in –ve y–direction and particle B is moving in +y–directionBThe particle B is moving in –ve y–direction and particle A is moving in +y–directionCBoth are moving in the +ve y–directionDBoth are moving in the –ve y–direction - Question 3 - Select One
Plane progressive wave y=Asin(ωt−kx) travels in positive X-direction with a speed
AωBωkCkxDv
A progressive wave is travelling along the positive direction of the x-axis. For this wave, amplitude = 5 cm, period = 0.2 s and wavelength = 30 cm
The equation of the wave using SI units is given byView SolutionA transverse wave travelling along the positive x-axis, given by y=Asin(kx−ωt) is superposed with another wave travelling along the negative x-axis given by y=Asin(kx+ωt). The point x=0 is
View SolutionThe equation of a plane progressive wave travelling along positive direction of x−axis is y=rsin[2πtT−2πxλ] where y= displacement of particle at (x,t),r= amplitude of vibratio of particle, T= time period of wave motion, λ= wavelength of wave ,x= starting distance of wave from the origin. Velocity of wave,
υ=vλ=λT= constant.
Acceleration of wave, a=0.
Velocity of particle at time t=dydt
Acceleration of particle at time t=d2ydt2
A harmonic wave travelling along positive direction of x axis is represented by
y=0.25×10−3sin(500t−0.025x)
where x and y are in metre and t is in second
The amplitude of vibration of particle isView SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by :-
_E01_059_Q01.png)
.View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by
View Solution