A cylindrical block floats vertically in a liquid of density ρ1 kept in a container such that the fraction of volume of the cylinder inside the liquid is x1. Then some amount of another immiscible liquid of density ρ2(ρ2<ρ1) is added to the liquid in the container so that the cylinder now floats just fully immersed in the liquids with x2 fraction of volume of the cylinder inside the liquid of density ρ1. The ratio ρ1/ρ2 will be
1−x2x1−x2
1−x1x1+x2
x1−x2x1+x2
x2x1−1
The correct Answer is:A
ρ1x1g=ρ1x2g+ρ2(1−x2)g
⇒ρ1ρ2=1−x2x1−x2.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - NCERT BASED QUESTIONS(FLUID FLOW)
51 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - PAST YEARS QUESTIONS
14 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
Similar Questions
An object of mass m is floating in a liquid of density σ. If the object is made up of density ρ, then appare weight of the object in the liquid is
View SolutionA body of density ρfloats with a volume V1 of its total volume V immersed in one liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2, where ρ1>ρ2. Find the relative volumes immersed in two liquids.
View Solution
Knowledge Check
A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
A(rho-rho_(1))/(rho_(2)-rho)Bρ2−ρρ−ρ1C(rho+rho_(1))/(rho+rho_(2))D(rho+rho_(2))/(rho+rho_(1))A wooden cylinder of length L is partly submerged in a liquid of specific gravity ρ1 with nth (n<1) part of it inside the liquid. Another immiscible liquid of density ρ2 is poured to completely submerge the cylinder. Density of cylinder ρ is the geometric mean of the densities of the two liquid.
Calculate the fraction of the cylinder submerged in the lower liquid after the upper liquid is poured in the vesselAn(n+1)B(n−1)(n+1)Cn(n−1)(n+1)Dn(n−1)(n+1)A block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
AρBρ3Cρ2D3ρ
A body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View Solution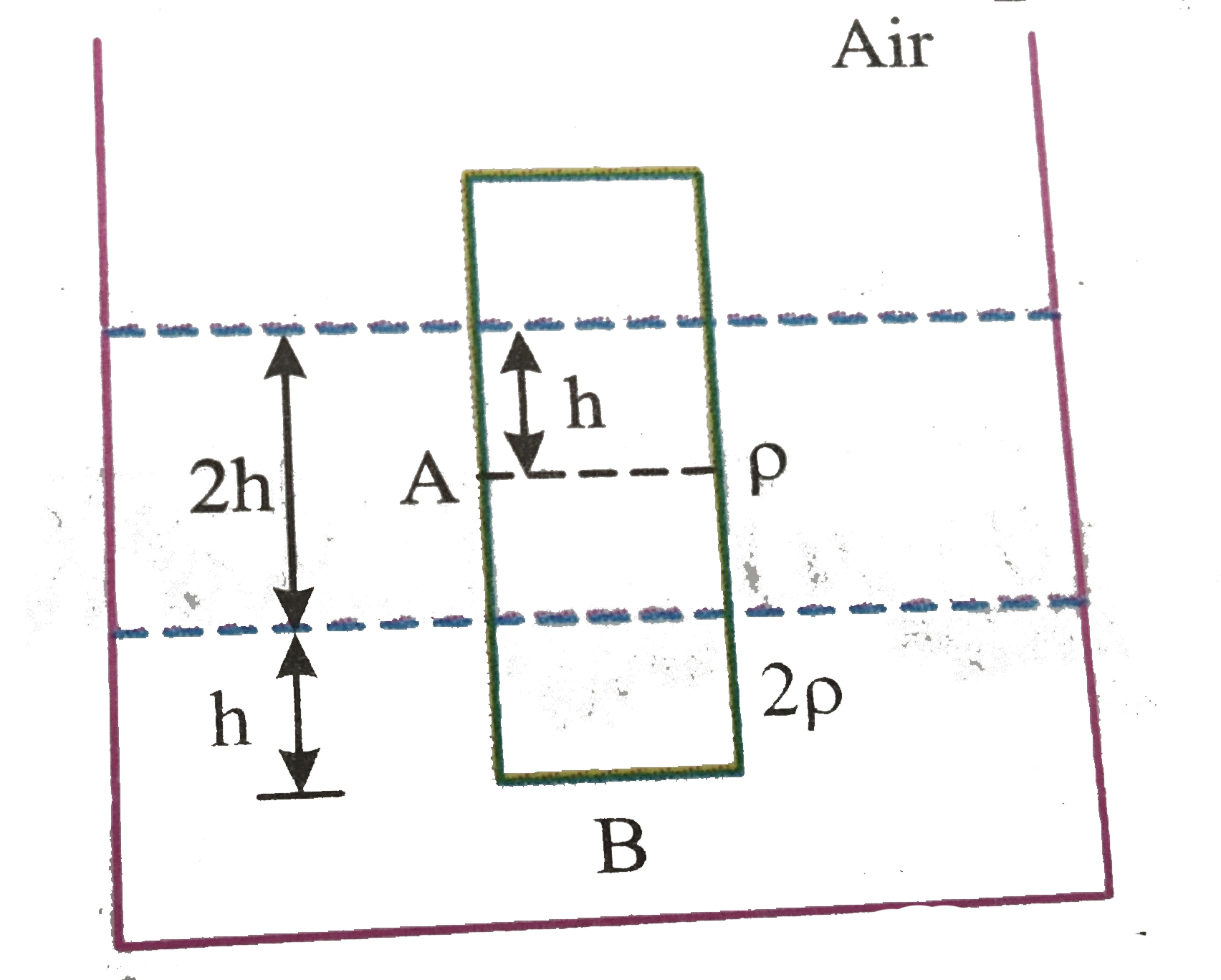
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:
View Solution
