A riding ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure below. The value of impulse imparted by the wall on the ball will be.

mv2
mv3
mV
2mV
The correct Answer is:C
∴Δ→V=−−−→Vfinal−−−−−→Vinitial
⇒−−→ΔV=(−Vcos60∘ˆi−Vsin60∘ˆj)
−(Vcos60∘ˆi−Vsin60∘ˆj)
⇒−−→ΔV=(−2Vcos60∘ˆi)
Thus impulse , I=m∣∣∣−−→ΔV∣∣∣
rArr I = m (2V cos 60
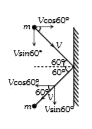
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION (MOTION OF CONNECTED BODIES)
22 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON
19 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
Similar Questions
A ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure.
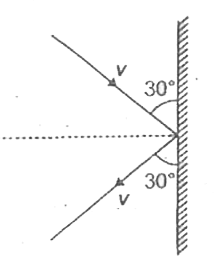
(a) What is the magnitude of the impulse imparted to the ball by the wall?
(b) What is the direction of the force on the wall due to the ball?
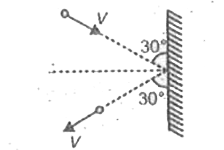
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View Solution
Knowledge Check
A rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
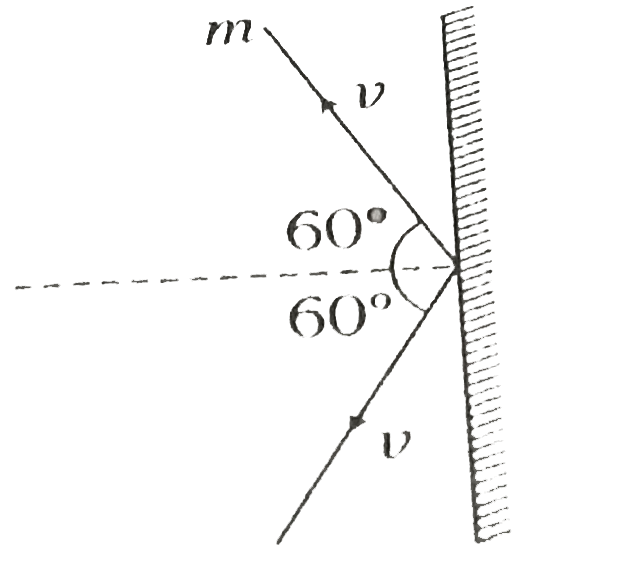 AmvB2mvCmv/2Dmv/3
AmvB2mvCmv/2Dmv/3A riding ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure below. The value of impulse imparted by the wall on the ball will be.
 AmV2BmV3C(mVD3mV
AmV2BmV3C(mVD3mVA ball of mass 'm' strikes a rigid wall with speed 'u' and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2 mu,Bmu,CzeroD−2mn
Two billiard balls of equal mass 30 g strike a rigid wall with same speed of 108 kmph (as shown) but at different angles. If the balls get reflected with the same speed then the ratio of the magnitude of impulses imparted to ball 'a' and ball 'b' by the wall along 'X' direction is
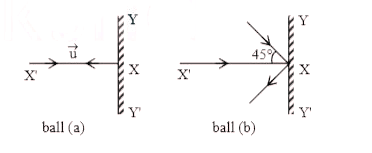
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
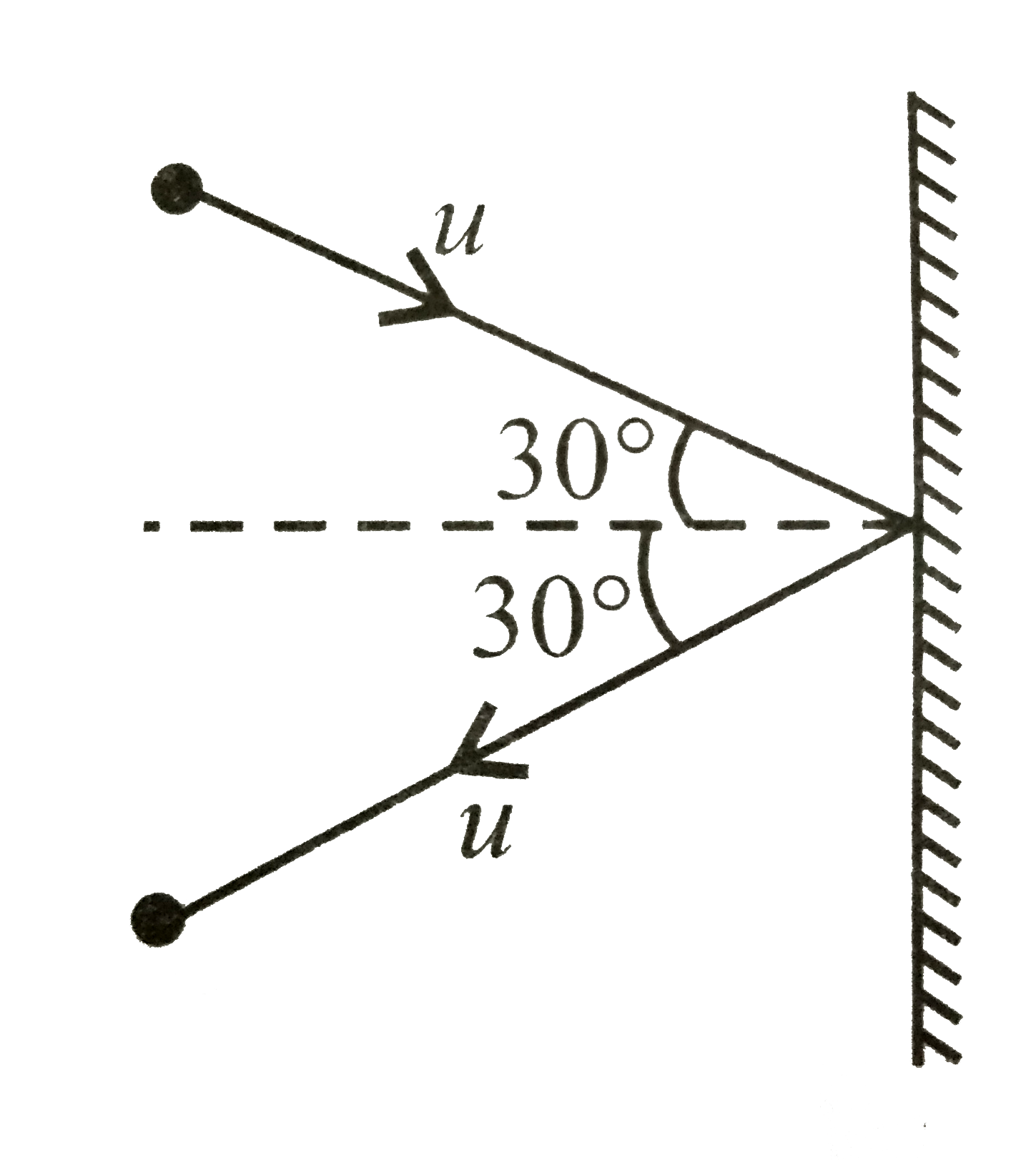
View SolutionA ball of mass 0.1 kg strikes a wall normally with a speed of 30ms−1 and rebounds with a speed of 20ms−1. The impulse of the force exerted by the wall on the ball is
View SolutionA ball of mass 0.2kg strikes an obstacle and moves at 60∘ to its original direction If its speed also changes from 20m/s to 10m/s, the magnitude of the impulse received by the ball is .
View Solution
