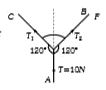
The adjacent figure is the part of a horizontally stretched net. section AB is stretched with a force of 10 N . The tensions in the sections BC and BF are

A

10 N, 11 N

B

10 N, 6 N

C

10 N, 10 N

D

Can't calculate due to insufficient data

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

From Lami.s theorem
$\frac{T_{1}}{{sin 120}^{\circ}} = \frac{T_{2}}{{sin 120}^{\circ}} = \frac{T}{{sin 120}^{\circ}}$
$\Rightarrow T = T_{1} = T_{2}$
$\Rightarrow T = 10 N$

Aliter :
$T_{1} {sin 60}^{\circ} = T_{2} {sin 60}^{\circ}$
$\Rightarrow T_{1} = T_{2}$
$2 T_{1} {cos 60}^{\circ} = T = 10$
$\Rightarrow T_{1} = T = 10 N = T_{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The adjacent figure is the part of a horizontally stretched net. Section AB is stretched with a force of 10 N. The tensions in the section BC and BF are

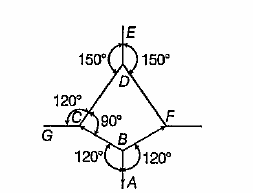A10 N, 11 N
B10 N,6 N
C10 N, 10 N
DCan't be calculated due to insufficient data
Question 2 - Select One
In figure, part of horizontal is stretched from A with force of 10 N. So, tension is the sections BC and BF is

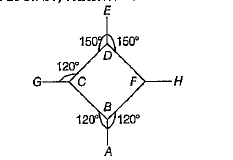A10N.11N
B10N,6N
C10N.10N
DNone of these
Question 3 - Select One
A wire of length 10 m and cross-section are $10^{- 6} m^{2}$ is stretched with a force of 20 N. If the elongation is 1 mm, the Young's modulus of material of the wire will be
A $10^{10} N / m^{2}$
B $10^{11} N / m^{2}$
C $2 \times 10^{10} N / m^{2}$
D $2 \times 10^{11} N / m^{2}$

ERRORLESS-NEWTON'S LAWS OF MOTION-NCERT BASED QUESTION ( SECOND LAW OF MOTION)

Home
Ask Doubt
Profile