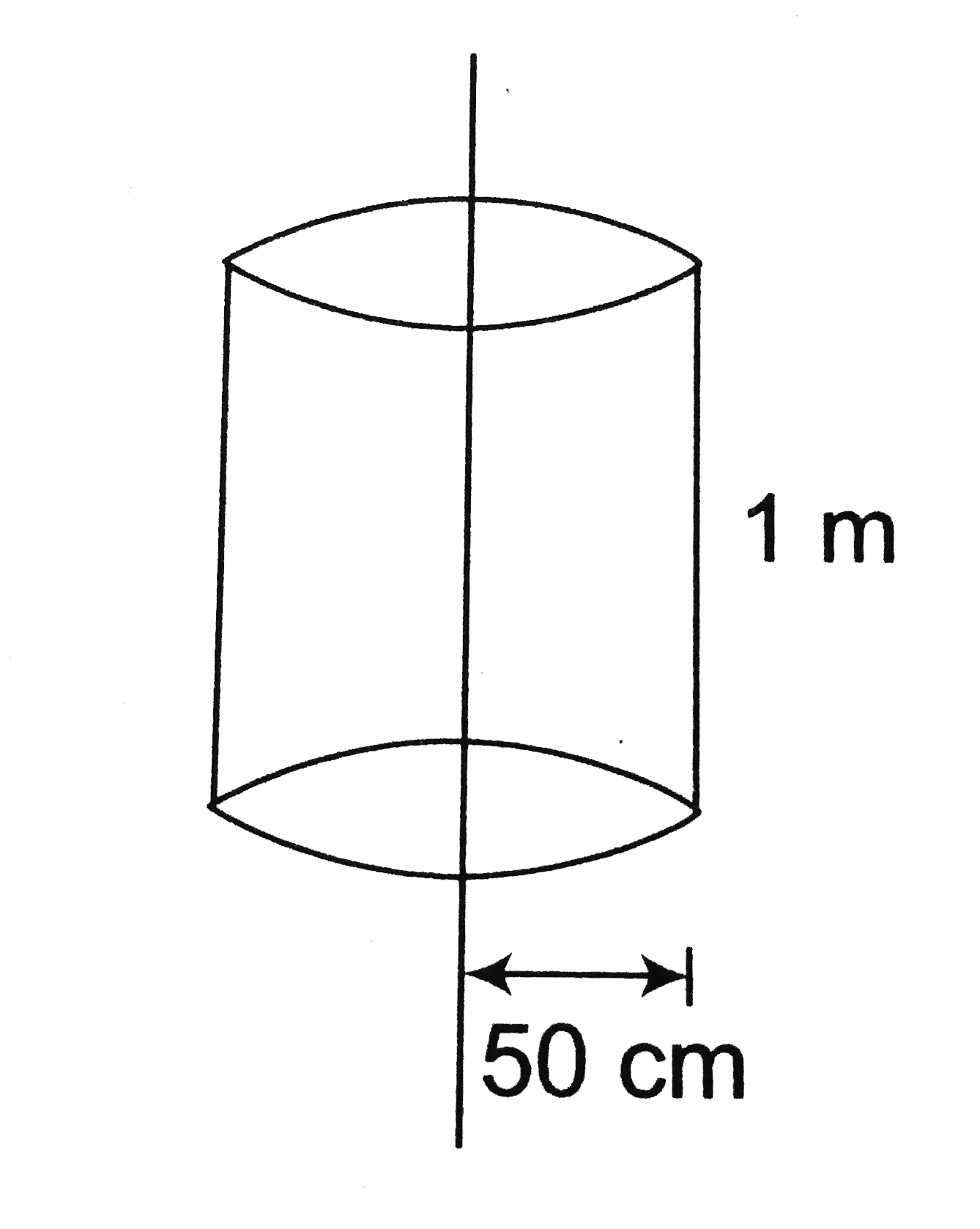
Electric charge is uniformly distributed along a along straight wire o

Electric charge is uniformly distributed along a long straight wire of radius 1 mm. The charge per cm length of the wire Q coulomb. Another cylindrical surface of radius 50 cm and length 1 m symmetrical encloses the wire as shown in the figure. The total electric flux passing through the cylindrical surface is
A $\frac{Q}{ε_{0}}$
B $\frac{100 Q}{ε_{0}}$
C $\frac{100 Q}{{(ε_{0})}_{0}^{2}}$
D $\frac{100 Q}{(π ε_{0})}$
An infinite, uniformly charged sheet with surface charge density $σ$ cuts through a spherical Gaussian surfance of radius $R$ at a distance $X$ from its center, as shown in the figure. The electric flux $Φ$ through the Gaussian surfce is .

A $\frac{π R^{2} σ}{ɛ_{0}}$
B $\frac{π {(R - x)}^{2} σ}{ɛ_{0}}$
C $\frac{π {(R - x)}^{2} σ}{ɛ_{0}}$
D $\frac{π (R^{2} - x^{2}) σ}{ɛ_{0}}$
A point charge causes an electric flux of $- 200 N m^{2} / C$ to pass through spherical Guassian surface of 10 cm radius centered on the charge. If the radius of the Guassian surface is doubled, the total electric flux passing through the surface is
A $- 200 N m^{2} / C$
B $- 100 N m^{2} / C$
C $+ 200 N m^{2} / C$
D $- 50 N m^{2} / C$

The correct Answer is:B